Математика в живых организмах

Кандидат биологических наук М. БЕРКИНБЛИТ,

кандидат педагогических наук Е. ГЛАГОЛЕВА

Живая природа сделала множество “изобретений”, которые люди поняли и смогли повторить лишь при соответствующем уровне развития науки и техники. Например, принцип эхолокации эффективно используют и дельфины, и летучие мыши, а в технике он появился только в XX веке; поиск добычи по инфракрасному излучению используют многие виды змей, в то время как очки для ночного видения созданы лишь недавно и т. д. До последнего времени бытовало убеждение, что природа не изобрела колеса, что здесь техника пошла своим оригинальным путем. Но оказалось, что жгутики бактерий вращаются в специальных “подшипниках” и, значит, колесо тоже “изобретено” природой еще на самых ранних этапах эволюции. Существует специальная наука — бионика, которая изучает “патенты природы”. Оказывается, что их можно иногда использовать и в “человеческой” технике.

Менее известно, что в живых организмах происходят явления, которые позволяют считать, что природе принадлежит “приоритет” и в создании своеобразных ЭВМ — устройств, производящих операции, весьма сходные с математическими операциями, которые мы склонны считать достижением  человеческой науки. Похоже, что здесь повторяется история с изобретением колеса.

О некоторых таких операциях мы и расскажем в этой статье: о том как “считают” нервные клетки, как “логарифмирует” глаз (и зачем ему это понадобилось), как оперирует с векторами и тригонометрическими функциями мозг кошки и обезьяны (и наш с вами тоже). Может быть, кто-нибудь решит, что и изучать эти вещи не надо, раз это дано от природы. А, может быть, некоторые — мы надеемся, что таких будет больше,— захотят узнать о математической и биологической стороне дела.

Как считают нейроны

Первое знакомство с математикой — это счет: “Раз, два, три, четыре, пять, вышел зайчик погулять”. И самым простым кажется и считается натуральное число. Уже отрицательные числа очень медленно входили в математику. Появившись в раннем средневековье у математиков Индии, они лишь в XIII—XIV веках проникают в европейскую науку, встречая там поначалу весьма сдержанное, отношение. Их называют “ложными”, “абсурдными” числами. Но постепенно отрицательные числа доказали свое право на существование и стали привычными не только для специалистов — то, что было “на переднем крае науки” в средние века, сегодня спокойно воспринимают пятиклассники.

А вот в живых организмах, оказывается “все наоборот”: нервной клетке (нейрону) естественно и просто осуществлять операции с положительными и отрицательными действительными “числами”, а для того чтобы “считать” даже до двух, требуется система из нескольких нейронов — примитивный “мозг”.

Как же работает нейрон? Как всякая клетка, нейрон отделен от наружной межклеточной среды особой оболочкой — мембраной. Между внутренним содержимым клетки и наружной средой существует разность потенциалов. Если клетка находится в покое, разность потенциалов на ее мембране не меняется. Эту разность потенциалов в покое естественно принять за нулевой уровень (подобно тому, как приняли за нулевую температуру таяния льда).

На нейрон могут действовать другие нервные клетки — возбуждающие и тормозные. Сигналы, полученные от этих клеток, вызывают изменения разности потенциалов на мембране в двух  противоположных направлениях. Когда разные сигналы приходят к нейрону одновременно, они складываются, причем, естественно, с учетом знака, т. е. нейрон суммирует приходящие к нему положительные и отрицательные сигналы; эта сумма может быть положительной или отрицательной.

Интересная особенность работы нейрона состоит в том, что в отличие от технических сумматоров — от древнего абака до ЭВМ — полученную сумму он “помнит” недолго: если внешние воздействия прекратились, то накопленная сумма начинает убывать по абсолютной величине, чтобы нейрон возвратился в состояние покоя (потенциал на мембране стремится к значению, которое мы приняли за нуль).

Такая вроде бы “ненадежность” нейрона связана с тем, что он предназначен не для хранения, а для передачи и преобразования информации : полученный сигнал нейрон передает другим клеткам нервной сети (клеткам-“мишеням” или “адресатам”). По способу передачи сигнала существуют два разных типа нейронов с разными принципами работы: “аналоговые” и “пороговые” нейроны.

Нейрон первого типа действует на клетки-мишени с силой, пропорциональной накопленной сумме, - но только в том случае, когда эта сумма положительна. Когда же сумма отрицательна, то она дальше не передается — нейрон заторможен. Правило преобразования сигналов аналоговыми нейронами описывается формулой, где х — накопленный потенциал, у — величина переданного сигнала, a k — коэффициент пропорциональности.

Нейроны второго типа работают иначе. Такой нейрон “молчит”, пока сумма воздействий не достигнет некоторой определенной положительной величины — “порога”. Тогда нейрон возбуждается и посылает по своему выходному отростку — аксону — электрический импульс (всегда одной и той же величины), который и действует на клетки-мишени. После возбуждения нейрон некоторое время “отдыхает” — молчит, независимо от того, действуют на него другие клетки или нет, а затем, если к концу отдыха накопленная сумма выше порога, посылает новый импульс. В результате в зависимости от величины входного сигнала, его длительности и в зависимости от характеристик нейрона на выходе получается сигнал в виде серии импульсов постоянной величины, но разной частоты. Таким образом, пороговые нейроны используют совершенно нетривиальный принцип кодирования информации частотой сигнала.

Однако, как и непрерывный выходной сигнал нейронов аналогового типа, изменение частоты несет информацию только о величине входного сигнала, меняющейся непрерывно. В то же время известно, что животные умеют считать (например, выдавать реакцию только на каждый третий стимул). Естественно предположить, что в нервной системе имеются устройства, которые по-разному реагируют, например, на двукратное воздействие и на однократное. То, что известно о принципах работы нейронов, позволяет утверждать: одиночной нервной клетке такая “простая” с человеческой точки зрения операция, как счет, не под силу. Недостаток места не позволяет нам описать устройство из нескольких нейронов, способное выдавать ответ, например, на каждый второй стимул.

Глаза и логарифмы

Зрительные рецепторы, так же, как и другие — слуховые, температурные и т. д., получают сигналы из внешнего мира; они должны передать зрительную информацию в мозг точно и своевременно. Передача сигналов от глаза к мозгу осуществляется нейронами “порогового” типа — аналоговый способ оказывается неприменимым при передаче сигналов на достаточно большие расстояния. А у пороговых нейронов, как уже говорилось, все импульсы совершенно одинаковы, и сведения о величине входного сигнала эти нейроны передают меняя частоту импульсации.

Тут возникает вот какая проблема. Освещенность в сумерках, когда предметы еле видны, отличается от освещенности при ярком солнечном свете примерно в миллиард (т. е. в 109) раз. Максимальная же частота, с которой может работать нейрон — 1000 импульсов в секунду. Легко сообразить, что нельзя передавать информацию, меняя частоту работы нейрона пропорционально освещенности: если при ярком свете частота импульсов будет максимальной (1000 имп/с), то при уменьшении освещенности в миллион раз сигнал будет поступать всего один раз в 15 минут. Но за это время он совершенно потеряет свою актуальность!

Но может быть, разумно такое устройство зрительной системы, когда разные ее элементы, разные нейроны работают каждый в своем диапазоне освещенности: одни в сумерки, другие в пасмурный день, третьи на ярком солнце. Простой подсчет показывает, что если принять за нижнюю границу частоты работы нейрона, необходимой для достаточно своевременной передачи информации, 1 имп/с, то для охвата диапазона изменения освещенности в миллиард раз потребуется миллион нейронов — и это без всякого “запаса” прочности, без дублирования их работы! Но главное вот что: в каждый момент будет работать только одна клетка из миллиона, а остальные 999 999 будут “даром есть хлеб”: ведь в отличие от технических, живые “механизмы” потребляют энергию (свой “бензин”) не только во время работы. А экономия энергии в живой природе — одно из главных условий выживания.

Итак, линейная зависимость между входными и выходными сигналами в случае глаза оказывается нецелесообразной. И действительно, в природе в этом случае используется другая функция, по школьным меркам довольно сложная.

Экспериментально это было установлено в 1932 году английским ученым X.Харлайном. На рисунке 1 приведены результаты его исследования. Он регистрировал нервные импульсы, идущие по одиночному нервному волокну от глаза к мозгу, у  мечехвоста (морского членистоногого, похожего на вымерших трилобитов). На графике показана зависимость частоты импульсации от яркости света.

“Но позвольте! — скажете вы.— На графике прямая линия — значит, это линейная функция”. Не торопитесь, вглядитесь в шкалу на горизонтальной оси, она ведь неравномерна, нелинейна: при сдвиге на одно деление аргумент (яркость) меняется не на одну и ту же величину, а в одно и то же число раз.

При линейной зависимости равным приращениям аргумента соответствуют равные приращения функции, или, что то же самое, линейная зависимость переводит арифметическую прогрессию значений аргумента в арифметическую же прогрессию значений функции. Когда мы имеем дело с показательной функцией у=ах, то равным приращениям аргумента соответствует равномерный относительный прирост функции. Например, при постоянных условиях обитания и неограниченных ресурсах так растет численность какой-либо популяции: число особей за каждый год увеличивается на 10%, т. е. в 1,1 раза. Другими словами, показательная функция “переводит” арифметическую прогрессию в геометрическую. На нашем графике ситуация обратная: частота импульсации нейрона меняется на одну и ту же величину, когда воздействие меняется в одно и то же число раз. Значит, мы имеем дело с функцией, обратной к показательной, т.е. с логарифмической; иными словами, нейроны глаза мечехвоста превращают геометрическую прогрессию раздражений в арифметическую прогрессию сигналов.

Это свойство зрительных рецепторов, выработавшееся в ходе эволюции, позволяет глазу работать эффективно и экономно, обеспечивает возможность хорошо воспринимать контраст. Пусть светлый и темный предметы различаются по способности отражать свет в десять раз. Тогда и на ярком солнце, и в сумерках светлый предмет будет отражать в десять раз больше света, чем темный. Поэтому сравнительная яркость этих предметов не меняется; не меняется и расстояние между соответствующими точками на оси абсцисс. А это означает, что разница частот работы рецепторов, на которые падает свет от этих двух предметов, будет оставаться неизменной при разных освещенностях. Так что “умение логарифмировать” позволяет глазу не только работать в широком диапазоне освещенностей, но и при малой освещенности различать предметы, абсолютная разность освещенностей которых очень мала.

Интересно, что описанная зависимость между внешним сигналом (раздражением) и сигналом, воспринимаемым мозгом (ощущением), первоначально была обнаружена психологами. Сделал это французский ученый П. Бугер еще в XVIII веке. В начале XIX века немецкий физиолог и психолог Э. Вебер детально изучил связь между раздражением и ощущением. Он выяснял, как нужно изменить какой-то раздражитель, чтобы человек заметил это изменение. Оказалось, отношение изменения величины раздражителя к его первоначальному значению есть величина постоянная:

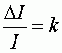, где I — мера раздражителя,— прирост раздражителя, a k — константа Вебера.

Константа Вебера зависит от того, какой рецептор раздражается. Например, при восприятии веса k=1/30. Это значит, что, когда человек держит груз в 100 г, он замечает его изменение при увеличении веса на 3,4 г, а для груза в 200 г требуется прибавка в 6,7 г. Для высоты звука константа Вебера равна 0,003, для громкости звука — 0,09 и т. д.

Рекомендуем скачать другие рефераты по теме: сообщение, закон реферат.





1  2  3 | Следующая страница реферата