
Элементарные финансовые расчеты
| Категория реферата: Рефераты по экономике
| Теги реферата: бесплатные рефераты и курсовые, реферат синдром
| Добавил(а) на сайт: Juhancev.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
Наряду с расчетом будущей и современной величины денежных средств часто возникают задачи определения других параметров финансовых операций: их продолжительности и величины процентной или учетной ставок. Например, может возникнуть вопрос: сколько времени понадобится, чтобы данная сумма при заданном уровне процентной ставки удвоилась, или при каком уровне учетной ставки в течение года исходная сумма возрастет в полтора раза? Решение подобных задач сводится к преобразованию соответствующей формулы наращения (дисконтирования) таким образом, чтобы вычислить значение неизвестного параметра. Например, если надо рассчитать продолжительность ссуды по известным первоначальной и будущей суммам, а также уровню простой процентной ставки, то преобразуя формулу начисления простых декурсивных процентов (S = P * (1 + ni)), получим формулу (5) из табл. 2.2.1. (Все формулы и их нумерация приведены в табл. 2.2.1). По такой же формуле будет определяться срок до погашения обязательства при математическом дисконтировании.
Определение срока финансовой операции для антисипативного начисления процентов и банковского учета производится по формуле (6) из табл. 2.2.1. Например, нужно определить через какой период времени произойдет удвоение суммы долга при начислении на нее 20% годовых простых а) при декурсивном методе начисления процентов; б) при использовании антисипативного метода. Временная база в обоих случаях принимается равной 365 дней (точные проценты). Применив формулы (5) и (6), получим:
а) t = (2 – 1) / 0,2 * 365 = 1825 дней (5 лет);
б) t = (1 – 1 / 2) / 0,2 * 365 = 912,5 дней (2,5 года)
Эти же формулы можно применить для определения срока до погашения обязательств при дисконтировании. Например, по векселю номиналом 700 тыс. рублей банк выплатил 520 тыс. рублей, произведя его учет по простой ставке 32% годовых. Чему равен срок до погашения векселя? Применив формулу (6), получим:
t = (1 – 520 / 700) / 0,32 * 360 = 289 дней
Товар, стоимостью 1,5 млн. рублей оплачивается на условиях коммерческого кредита, предоставленного под 15% годовых (простая процентная ставка, временная база 360 дней). Сумма оплаты по истечении срока кредита составила 1 млн. 650 тыс. рублей. Чему равен срок предоставленного кредита? Из формулы (5) следует:
t = (1,65 / 1,5 – 1) / 0,15 * 360 = 240 дней
Таблица 2.2.1
Формулы расчета продолжительности финансовых операций и процентных (учетных) ставок по ним
|
Способ начисления процентов |
Продолжительность ссуды |
Процентная (учетная) ставка |
|
|
1. Простые декурсивные проценты (t – длительность в днях, K – временная база) |
|
|
|
|
2. Простые антисипативные проценты (t – длительность в днях, K – временная база) |
|
|
|
|
3. Сложные декурсивные проценты проценты по эффективной ставке i (n – длительность, лет) |
|
|
|
|
4. Сложные декурсивные проценты по номинальной ставке j (n – длительность, лет) |
Рекомендуем скачать другие рефераты по теме: курсовая работа 2011, культурология. Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
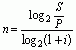 (7)
(7)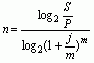 (8)
(8) Главная
Главная