|
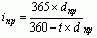 (36) (36)
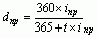 (37) (37)
|
–
|
Например, предприятие может столкнуться с необходимостью выбора между получением кредита
на 5 месяцев под сложную номинальную ставку 24% (начисление процентов
поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком
погашения. Небходимо определить простую учетную ставку, которая сделает учет
векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26)
получим d = 22,21%.
Кроме
формул, приведенных в табл. 3.2.2 и 3.2.3, следует отметить еще одно полезное
соотношение. Между силой роста и дисконтным множителем декурсивных процентов
существунт следующая связь:
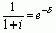 (38)
(38)
По
мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения
непрерывных процентов будет расширяться, так как при этом становится возможным
использовать более мощный математический аппарат. Особенно наглядно это
проявляется в случае непрерывных процентных ставок. В обыденной практике
финансистов данный способ пока еще не занял должного места, что в какой-то мере
объясняется его непривычностью, может быть чересчур “отвлеченным” характером.
Однако трезвый анализ показывает, что предположение о непрерывности реинвестирования
начисленных процентов не такое уж абстрактное и нереальное. В самом деле, как
для простых, так и для сложных процентов факт непрерывности их начисления ни у
кого не вызывает сомнений (годовая ставка 36% означает 3% в месяц, 0,1% в день
и т.д., то есть можно начислять проценты хоть за доли секунды). Но точно такой
же аксиомой для финансов является признание возможности мгновенного
реинвестирования любых полученных сумм. Что же мешает совместить два этих
предположения? В теории сумма начисленных процентов может (и должна)
реинвестироваться сразу по мере ее начисления, т.е. непрерывно. В данном
утверждении ничуть не меньше логики, чем в предположении, что реинвестирование
должно производиться дискретно. Почему реинвестирование 1 раз в год считается более
“естественным” чем 12 или 6 раз? Почему эта периодичность привязывается к
календарным периодам (год, квартал, месяц), почему нельзя реинвестировать
начисленные сложные проценты, скажем 39 раз в год или 666 раз за период между
двумя полнолуниями? На все эти вопросы ответ, скорее всего, будет один – так
сложилось, так привычно, так удобнее. Но выше уже было отмечено, что
практический расчет величины реальных денежных потоков (например, дивидендных
или купонных выплат) и определение доходности финансовых операций это далеко не
одно и то же. Если привычнее и удобнее выплачивать купон по облигации 2 раза в
год, то так и следует поступать. Но, определять доходность этой операции более
логично по ставке непрерывных процентов.
Таблица
2.2.3
Эквивалентность
сложных процентных ставок
|
|
Сложная процентная ставка
(iсл)
|
Сложная учетная ставка
(dсл)
|
|
Сложная номинальная процентная
ставка (j)
|
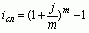 (39) (39)
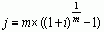 (40) (40)
|
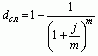 (41) (41)
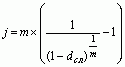 (42) (42)
|
|
Сила роста (d)
|
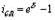 (43) (43)
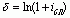 (44) (44)
|
Сложная номинальная процентная
ставка (j)
|
|
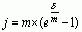 (45) (45)
Рекомендуем скачать другие рефераты по теме: курсовая работа 2011, культурология.
Предыдущая страница реферата | 1
2
3
4
5
6
7 | Следующая страница реферата
|
|

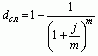 (41)
(41) 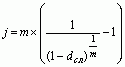 (42)
(42)  Главная
Главная