|
0
|
|
|
4
|
01
|
-
|
1
|
3
|
|
|
5
|
0
|
1
|
-
|
0
|
|
|
6
|
3
|
3
|
01
|
-
|
|
|
табл. 8
|
Дополнительно в
уменьшенной матрице поставлен запрет в клетке (2,1), т. к. выбрано ребро (1,2)
и замыкать преждевременно тур ребром (2,1) нельзя. Уменьшенную матрицу можно
привести на 1 по первому столбцу, так что каждый тур, ей отвечающий, стоит не
меньше 35. Результат наших ветвлений и получения оценок показан на рис.6.
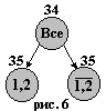 Кружки представляют классы: верхний кружок
– класс всех туров; нижний левый – класс всех туров, включающих ребро (1,2);
нижний правый – класс всех туров, не включающих ребро (1,2). Числа над кружками
– оценки снизу.
Кружки представляют классы: верхний кружок
– класс всех туров; нижний левый – класс всех туров, включающих ребро (1,2);
нижний правый – класс всех туров, не включающих ребро (1,2). Числа над кружками
– оценки снизу.
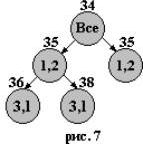 Продолжим ветвление в положительную сторону: влево - вниз. Для
этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в
клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7
есть 35+3=38. Для оценки левой нижней вершины на рис. 7 нужно вычеркнуть из
матрицы C[1,2] еще строку 3 и
столбец 1, получив матрицу C[(1,2),(3,1)] на табл. 8. В эту матрицу нужно поставить запрет в
клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е.
[3,1,2], и нужно запретить преждевременное замыкание (2,3). Эта матрица
приводится по столбцу на 1 (табл. 9), таким образом, каждый тур
соответствующего класса (т.е. тур, содержащий ребра (1,2) и (3,1)) стоит 36 и
более.
Продолжим ветвление в положительную сторону: влево - вниз. Для
этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в
клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7
есть 35+3=38. Для оценки левой нижней вершины на рис. 7 нужно вычеркнуть из
матрицы C[1,2] еще строку 3 и
столбец 1, получив матрицу C[(1,2),(3,1)] на табл. 8. В эту матрицу нужно поставить запрет в
клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е.
[3,1,2], и нужно запретить преждевременное замыкание (2,3). Эта матрица
приводится по столбцу на 1 (табл. 9), таким образом, каждый тур
соответствующего класса (т.е. тур, содержащий ребра (1,2) и (3,1)) стоит 36 и
более.

 Кружки представляют классы: верхний кружок
– класс всех туров; нижний левый – класс всех туров, включающих ребро (1,2);
нижний правый – класс всех туров, не включающих ребро (1,2). Числа над кружками
– оценки снизу.
Кружки представляют классы: верхний кружок
– класс всех туров; нижний левый – класс всех туров, включающих ребро (1,2);
нижний правый – класс всех туров, не включающих ребро (1,2). Числа над кружками
– оценки снизу. Продолжим ветвление в положительную сторону: влево - вниз. Для
этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в
клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7
есть 35+3=38. Для оценки левой нижней вершины на рис. 7 нужно вычеркнуть из
матрицы C[1,2] еще строку 3 и
столбец 1, получив матрицу C[(1,2),(3,1)] на табл. 8. В эту матрицу нужно поставить запрет в
клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е.
[3,1,2], и нужно запретить преждевременное замыкание (2,3). Эта матрица
приводится по столбцу на 1 (табл. 9), таким образом, каждый тур
соответствующего класса (т.е. тур, содержащий ребра (1,2) и (3,1)) стоит 36 и
более.
Продолжим ветвление в положительную сторону: влево - вниз. Для
этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в
клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7
есть 35+3=38. Для оценки левой нижней вершины на рис. 7 нужно вычеркнуть из
матрицы C[1,2] еще строку 3 и
столбец 1, получив матрицу C[(1,2),(3,1)] на табл. 8. В эту матрицу нужно поставить запрет в
клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е.
[3,1,2], и нужно запретить преждевременное замыкание (2,3). Эта матрица
приводится по столбцу на 1 (табл. 9), таким образом, каждый тур
соответствующего класса (т.е. тур, содержащий ребра (1,2) и (3,1)) стоит 36 и
более. Главная
Главная