если bk>bj+djk то (bk:=bj+djk; ck:=j) {Условие означает, что путь vi..vk длиннее, чем путь vi..vj,vk . Если все a[k] отмечены, то длина пути vi..vk равна b[k]. Теперь надо перечислить вершины, входящие в кратчайший путь} 3(выдача ответа). {Путь vi..vk выдаётся в обратном порядке следующей процедурой:} 3.1. z:=c[k]; 3.2. Выдать z; 3.3. z:=c[z]; Если z = 0, то конец, иначе перейти к 3.2. Для выполнения алгоритма нужно n раз просмотреть массив b из n элементов, т. е. 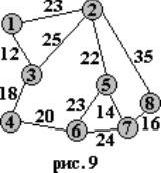алгоритм Дейкстры имеет квадратичную сложность. Проиллюстрируем работу алгоритма Дейкстры численным примером (для большей сложности, считаем, что некоторые города (вершины) i,j не соединены между собой, т. е. D[i,j]=∞). Пусть, например, i=3. Требуется найти кратчайшие пути из вершины 3. Содержимое массивов a,b,c после выполнения первого пункта показано на табл. 12:
|
Главная