Микроэкономика: межвременной выбор

Введение

Часто при рассмотрении задач мы предполагали, что экономические действия и их последствия относятся к одному и тому же моменту времени. Как бы ни были полезны для понимания экономических проблем модели, в которых отсутствует время, реальный мир таков, что события и процессы в нем привязаны ко времени. Килограмм яблок, имеющийся в распоряжении потребителя сегодня, — это не тоже самое, что килограмм таких же яблок, который достоверно будет у него в следующем месяце. Экономические блага различаются не только своими физическими свойствами, как например яблоки, пирожки с мясом и джинсы, но и принадлежностью к определенному моменту времени (периоду). Это обстоятельство имеет важные последствия для потребительского выбора и экономики в целом.

Бюджетное ограничение

Для наглядной иллюстрации, упростим ситуацию, введя модель. Разобьем весь временной промежуток на два – настоящее и будущее. Делая свой выбор, семья должна рассчитать наперед доход, который она предполагает получить в будущем, а также оценить потребление товаров и услуг, которое она сможет себе позволить при своих доходах.

Представим себе потребителя, который решает, сколько данного товара потребить в каждом из двух временных периодов. Будем считать такой товар композитным либо конкретным товаром. Обозначим величину потребления в каждом периоде через (с1,c2) и предположим, что цены потребления в каждом периоде постоянны и равны 1. Сумму денег, имеющуюся у потребителя в каждом периоде, обозначим через (m1, m2)-

Вначале предположим, что единственный способ, которым потребитель может перевести деньги из периода 1 в период 2, — это сбережение денег без получения процента. Более того, пока предположим, что у него нет возможности занимать деньги, так что максимальная сумма, которую он может истратить в периоде 1, есть m1. Тогда его бюджетное ограничение будет иметь следующий вид:

Это бюджетное ограничение для случая, когда ставка процента равна нулю и брать деньги взаймы не разрешается. Чем меньше потребит данный индивид в период 1, тем больше он может потребить в период 2.Мы видим, что у потребителя имеется выбор двоякого рода. Он может предпочесть потреблять в точке (m1,m2), что означает просто потребление своего дохода в каждом периоде, или же может предпочесть потребить в периоде 1 не весь свой доход. В этом последнем случае потребитель откладывает часть потребления первого периода на более позднее время.

Теперь позволим потребителю брать и давать взаймы по некой ставке процента r. Сохраняя для удобства цены потребления в каждом периоде на уровне I, выведем уравнение бюджетного ограничения. Сначала допустим, что потребитель решает делать сбережения, так что величина его потребления в первом периоде q меньше дохода первого периода т1. В этом случае он заработает процент на сберегаемую им сумму m1—c1 исходя из ставки процента r. Сумма, которую он может израсходовать на потребление в следующем периоде, задана выражением

с2 = m2 + (m1—С1) + r(m1 — c2)

= m2+ (1 + r) (m1 –c1).

В периоде 2 потребитель может истратить на потребление сумму, равную его доходу плюс сумма сбережений, сделанных в период 1, плюс процент, заработанный на эти сбережения.

Предположим теперь, что потребитель является заемщиком, так что его потребление в первом периоде превышает его доход первого периода. Потребитель выступает заемщиком, если с2 > m1, и процент, который ему придется платить во втором периоде, составит r(m1 — c1). Разумеется, ему придется также вернуть и взятую взаймы сумму, c1—m1 . Это означает, что его бюджетное ограничение задано уравнением

с2 = m2— r(с1 — m1) — (c1 — m1) = m2+ (1 + r) (m1 –c1),

что в точности совпадает с уравнением, записанным выше. Если величина m1 — c1 положительна, то потребитель зарабатывает процент на эти сбережения; если же эта величина отрицательна, потребитель платит процент на взятую взаймы сумму.

Если с1 = m1 то с необходимостью с2 > m2 потребитель не является ни заемщиком, ни кредитором.

Можно преобразовать уравнение бюджетного ограничения для данного потребителя, получив два полезных альтернативных вида этого уравнения:

(1 + r) c1 + с2 = (1 + r) m1 + m2 (цена будущего потребления равна 1)

и

c1+c2/1+r=m1+m2/1+r (цена текущего потребления равна 1)

В первом уравнении бюджетного ограничения цена потребления первого периода измерена относительно цены потребления второго периода, а во втором уравнении — наоборот.

Оба уравнения имеют форму

p1x1+p2x2=p1m1+p2m2

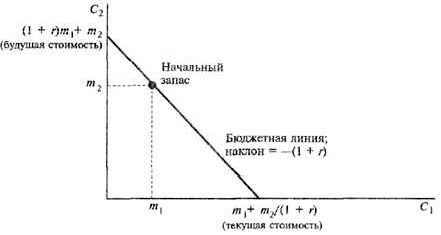
Геометрическая интерпретация текущей и будущей стоимостей дана на рис. 10.2. Текущая стоимость начального запаса денег в двух периодах есть сумма денег в периоде 1, которая породила бы то же самое бюджетное множество, что и начальный запас денег. Эта сумма, показанная просто точкой пересечения бюджетной линии с горизонтальной осью, дает максимально возможную в первом периоде величину потребления. Как показывает бюджетное ограничение, эта сумма есть с1= m1 + m2(1+r), что составляет текущую стоимость начального запаса.

Предпочтения в отношении потребления

Аналогично точка пересечения бюджетной линии с вертикальной осью показывает максимальную сумму, расходуемую на потребление во втором периоде, которая соответствует c1 = 0. И опять из уравнения бюджетного ограничения мы можем найти эту величину с2— (1+r)m1 + m2, представляющую собой будущую стоимость начального запаса.

Рекомендуем скачать другие рефераты по теме: диплом формирование, научные статьи.





1  2  3  4 | Следующая страница реферата