Claw.ru | Рефераты по философии | Человечество. Некоторые нестандартные модели Человечество. Некоторые нестандартные модели | Категория реферата: Рефераты по философии | Теги реферата: реферат на тему политика, реферати українською | Добавил(а) на сайт: Rokossovskij. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

3. Простейшая модель роста параметра целого человеческой популяции

Хотя, в действительности, процесс изменения числа живущих на Земле людей происходит дискретно, с рождением каждого человека число людей увеличивается на единицу, однако это число настолько велико, что процесс его изменения в первом приближении может считаться непрерывным.

Тем самым, изменения числа людей может быть описано некоторым дифференциальным уравнением, общий вид которого

.

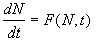Так как человечество развивается, по-видимому, в основном, по своим внутренним законам, то изменение его параметра целого может описываться автономным уравнением, в котором 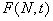является функцией только от 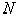и уравнение динамики параметра целого принимает вид

.

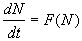Конечно, на развитие человечества оказывают влияние различные факторы. однако, если человечество считать системой, развивающейся по единому закону, то этот закон должен быть связан с основным свойством человеческой популяции, а именно с половым характером размножения. В соответствии с половым характером размножения все люди делятся на две половины - мужчин и женщин,- при этом каждый мужчина может в принципе, образовать пару с любой женщиной, и результатом этой пары может быть рождение ребенка. Естественно, такие возможности не осуществляются всегда, однако это можно учесть введением некоторого коэффициента. При таком наиболее естественном предположении вид функции 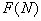существенно упрощается и принимает вид. [25]:

,

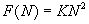а само дифференциальное уравнение получает форму

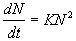(3.1)

В монографии [10] дано иное обоснование целесообразности применения этого уравнения на довольно длительном интервале существования человеческой популяции.

“Отмеченный кооперативный закон роста ( удовлетворяющий уравнению (3.1)) в значительной мере является прямым выражением информационной природы развития. Распространение и передача из поколения в поколение информации – знаний и технологий, обычаев и культуры, религии и, наконец, представлений науки есть то, что качественно отличает человека и человечество в своем развитии от животного мира. [28 ], [21 ], [29]. …

Такая зависимость возникает потому, что при обмене и распространении информации происходит умножение числа её` носителей в результате разветвленной цепной реакции. Обмен и распространение информации отличается от эквивалентного обмена ценностями, когда, например, при обмене невесты на стадо баранов общее число объектов обмена сохраняется. Разница удачно выражена в анекдоте о том, как хорошо обмениваться идеями: при этом каждый приобретает по идее, ничего не теряя. Очевидно, что распространение информации необратимо – слово не воробей, вылетит не поймаешь! С другой стороны, обмен товарами принципиально обратим.

Сейчас принято выделять информационную составляющую современной цивилизации. Но следует подчеркнуть, что человечество всегда было информационным обществом. Иначе трудно понять природу квадратичного роста, так отличающего человека от остальных животных”

(А существует ли это отличие? Ведь все известные нам виды многоклеточных животных, кроме домашних, либо уже стабилизировали свою численность, либо исчезают под влиянием человека. Так что не с чем сравнивать.).

Получим решение этого дифференциального уравнения.

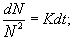
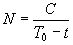
В эту формулу входят два произвольных параметра, которые должны быть константами динамики человечества. Физический смысл параметра 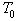-более не менее ясен. Это тот момент времени, когда, в случае сохранения гиперболического закона роста человеческой популяции, число людей стало бы равным бесконечности. Такой режим теоретически предсказывается во многих задачах, связанных с горением и является типичным при исследовании проблем самоорганизации. Кроме того, подобный режим встречается также при исследовании резонансных явлений [34]. Реально он, естественно никогда не осуществляется, однако связанные с ним тенденции гиперболического роста основного параметра системы реализуются вплоть до очень высоких значений параметра целого. Однако момент, когда возникает взрыв, определяется параметром 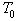с достаточной степенью точности.

Сопоставление этой математической модели с экспериментальными данными, выполненное в [10], не только подтвердило универсальность указанного простого закона, не только позволило более точно определить момент времени 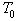, но и вычислить другую константу 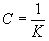. Самое удивительное, что рост человеческой популяции удовлетворял этому закону практически все 200000 лет, в течение которых существовало человечество. Отклонение от него началось лишь в конце семидесятых- начале восьмидесятых годов двадцатого века.

4. Модель роста комплексного параметра целого человеческой популяции. Демографический переход как вихревая особенность в поле комплексного времени.

Если идею о комплексификации параметра целого [18], [34] описывающего размножающиеся объекты применить к человечеству как к единой системе, то для описания динамики роста человеческой популяции можно ввести некое комплексное число 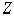, действительная часть которого характеризует рассмотренный выше параметр целого человечества и может быть приравнена к числу людей 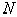, а мнимая часть может характеризовать информационный параметр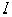

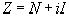
Представленная в [10 ], [21 ] и частично приведенная выше экспериментальная зависимость 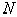от времени может служить исходным материалом, который позволил бы нам подобрать соответствующую простую комплексную функцию 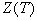. При этом время 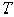также целесообразно считать комплексной величиной

.

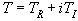То есть, на наш взгляд, важной задачей исследователя человеческого общества является отыскание такой простой комплексной функции от времени, действительная часть которой достаточно адекватно описывала бы имеющуюся экспериментальную зависимость 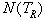. Как следует из приближенного анализа имеющихся экспериментальных данных, в течение очень долгого промежутка времени рост числа людей происходил по единому закону

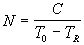, (4.1)

Рекомендуем скачать другие рефераты по теме: реферат китай курсовые работы, бесплатные шпаргалки по праву.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата