Расчет неупорядоченных площадных систем

Р.С.Шенгелов

Теперь рассмотрим особенности расчетов неупорядоченных площадных систем. Очень часто системы водозаборных скважин имеют именно такой характер: в силу особенностей условий строительства и землепользования, исторически сложившиеся и т.д. Их точный расчет всегда возможен по принципу суперпозиции (суммирования взаимодействий), но это может быть очень громоздко и трудоемко при выполнении многовариантных расчетов, так как количество скважин в системе может достигать десятков и даже сотен. Поэтому нередко используют методику приближенного расчета крупных площадных систем взаимодействующих скважин, который бывает вполне достаточен для решения двух важных задач:

а) расчет влияния таких систем на некоторые удаленные от них точки (почему-либо интересные - например, на соседний водозабор);

б) предварительная оценка возможного суммарного дебита таких систем. 

Для приближенного расчета площадных систем используют идею "БОЛЬШОГО КОЛОДЦА", под которым понимается одна-единственная скважина с большим радиусом , эквивалентная всей системе, т.е. имеющая тот же суммарный дебит и дающая те же понижения в области влияния. Наиболее чисто этот прием обосновывается при отсутствии близкорасположенных границ - например, для "схемы Тейса".

Система состоит из  скважин с разными дебитами  и разным временем ввода в действие  для каждой скважины (рис.1).

Рис. 1.

 Определим по принципу сложения решений понижение уровня в некоторой точке в момент t, полагая, что расчетное время достаточно для наступления квазистационарного режима в точке:

(введем долевые коэффициенты дебита )

.

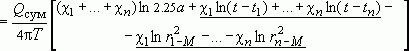Учитывая, что, а две подчеркнутые группировки однородных членов можно свернуть по свойствам логарифма:

,

,

получим окончательное выражение в виде:

.

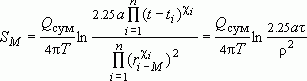Видно, что полученное выражение для  по форме аналогично действию одной скважины, находящейся на расчетном расстоянии  от точки  и действующей с суммарным дебитом  в течение расчетного времени . Такая скважина и называется "большим колодцом". Некоторые комментарии:

В частном случае равнодебитных скважин () долевые коэффициенты также равны между собой; тогда  

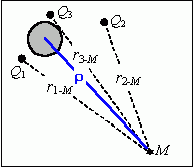
Очевидно, что при такой методике расчета  физическое положение "большого колодца" в принципе безразлично; важно только, что он находится на расчетном расстоянии. Можно использовать и другую методику, не требующую специального вычисления : предварительно рассчитывается положение центра (оси) "большого колодца" как центра тяжести системы скважин по их расходам, от которого и измеряется расчетное расстояние до точки (рис. 2).

Координаты центра "большого колодца" в произвольной системе декартовых координат {X,Y} вычисляются с учетом координат и долевых коэффициентов дебита каждой скважины:

.

По численным оценкам, погрешность расчетов понижений не превышает 3-5% для точек, удаленных от площадки системы скважин на расстояние, превышающее ее наибольший размер.

Другая полезная практическая задача: оценка возможного суммарного притока к системе скважин. Для этого рассчитывается радиус "большого колодца" , т.е. точка перемещается на стенку "большого колодца". При этом одна из скважин принимается за опорную и от нее рассчитываются расстояния до всех остальных; после этого оценивается

Рекомендуем скачать другие рефераты по теме: военные рефераты, контрольные за 1 полугодие.





1  2  3 | Следующая страница реферата