Предыдущая страница реферата | 1  2  3  4

Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен d - импульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.[3]

Из определения дельта-функции следует (3) . Следовательно, интеграл дельта-функции от - ¥ до t есть единичный скачок , и дельта-функцию можно рассматривать как производную единичного скачка :

 d(t) = 1’ (t) ;

d(t-t0) = 1’ (t-t0) .

Обобщенные функции как математические модели сигналов.

В классической математике полагают, что функция S(t) должна принемать какие-то значения в каждой точке оси t . Однако рассмотренная функция d(t) не вписывается в эти рамки - ее значение при t = 0 не определено вообще, хотя эта функция и имеет единичный интеграл. Возникает необходимость расширить понятие функции как математической модели сигнала. Для этого в математике была введено принципиально новое понятие обобщенной функции.

 В основе идеи обобщенной функции лежит простое интуитивное соображение. Когда мы держим в руках какой-нибудь предмет , то стараемся изучить его со всех сторон, как бы получить проекции этого предмета на всевозможные плоскости. Аналогом проекции исследуемой функции ¦(t) может служить, например, значение интеграла

 ¥

 ò ¦(t) j(t) dt (8)

 - ¥

при известной функции j(t) , которую называют пробной функцией.

Каждой функции j(t) отвечает, в свою очередь, некоторое конкретное числовое значение. Поэтому говорят, что формула (8) задает некоторый функционал на множестве пробных функций j(t). Непосредственно видно, что данный функционал линеен, то есть

 (¦, aj1 + bj2) = a(¦,j1) + b(¦,j2).

Если этот функционал к тому же еще и непрерывен, то говорят, что на множестве пробных функций j(t) задана обобщенная функция ¦(t) [4] . Следует сказать, что данную функцию надо понимать формально-аксиоматически, а не как предел соответствующих интегральных сумм.

Обобщенные фнкции , даже не заданные явными выражениями, обладают многими свойствами классических функкций. Так, обобщенные функции можно дифференцировать.

И в заключение следует сказать, что в настоящее время теория обобщенных функций получила широкое развитие и многочисленные применения. На ее основе созданы математические методы изучения процессов, для которых средства классического анализа оказываются недостаточными.

Список литературы

1. А. Л. Зиновьев, Л. И. Филипов ВВЕДЕНИЕ В  ТЕОРИЮ СИГНАЛОВ И ЦЕПЕЙ.

2. С. И. Баскаков РАДИОТЕХНИЧЕСКИЕ ЦЕПИ  И СИГНАЛЫ.

[1] Также эту функцию называют единичной импульсной функцией,

[2] Говорят, что дельта-функция сосредоточена в этой точке.

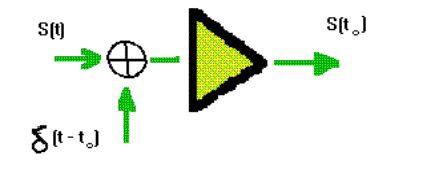
[3] Отсюда вытекает структурная схема систем, осуществляющей измерение мгновенных значений аналогового сигнала S(t). Система состоит из двух звеньев : перемножителя и интегратора.

[4] Обобщенные функции иногда называют также распределениями.

Скачали данный реферат: Krylov, Amelfa, Набатников, Burkin, Jaminskij, Фиста, Ясевич.
Последние просмотренные рефераты на тему: класс, море реферат, реферат связь, конспект урока по математике.





Предыдущая страница реферата | 1  2  3  4