Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

n=2:  y(0T) = x(0T)h(2T) + x(1T)h(1T) + x(2T)h(0T) + x(3T)h(-1T) = 0,168;

n=3:  y(0T) = x(0T)h(3T) + x(1T)h(2T) + x(2T)h(1T) + x(3T)h(0T) = -0,016;

Следовательно y(nT)= {0; 0,4; 0,168; -0,016}, что совпадает с расчётами по линейной свёртке в примере параграфа 2.4.

Графики периодических числовых последовательностей x(nT), h(nT), y(nT) приведены на рис.(2.7).

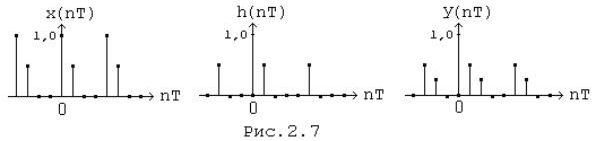
К периодическим числовым последовательностям, полученным изложенным выше способом, можно применить ДПФ, перемножить результаты и после выполнения обратного ДПФ получить последовательность y(nT), совпадающую с результатами расчётов по круговой свёртке.

Энергия дискретного сигнала

Корреляция и энергетический спектр.

В качестве энергии дискретного сигнала принята мера

Wx =x2(nT), (2.15)

соответственно в частотной области, согласно равенству Парсеваля,

Wx =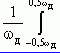X2(w)dw =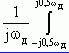X(jw)X*(jw)d(jw), (2.16)

где X(jw) = X(w)ejj(w) - спектр сигнала x(nT),

X*(jw) = X(w)e-jj(w) - спектр x(-nT) в соответствии с теоремой о спектре инверсного сигнала,

X2(w) = X(jw)ЧX*(jw) = Sx(jw) - энергетический спектр сигнала x(nT).

На рис.(2.8) показан в качестве примера сигнал x(nT) и его инверсная копия x(-nT) для некоторого частного случая

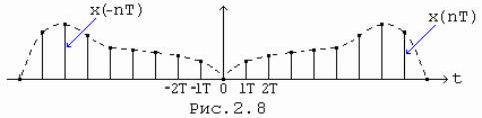
Энергетический спектр выражает среднюю мощность сигнала x(nT), приходящуюся на узкую полосу частот в окрестности переменной w.

Во временной области энергетическому спектру соответствует свертка инверных сигналов, что определяет корреляционную функцию Sx(nT) сигнала x(nT).

.  (2.17)

Согласно (2.17) и (2.15) корреляционная функция в точке n = 0 равна энергии сигнала, т. е.

 (2.18)

Для периодических дискретных сигналов корреляционная функция и энергетический спектр связаны формулами ДПФ

. (2.19)

Отсюда получаются расчётные формулы энергии периодических дискретных последовательностей

, (2.20)

Рекомендуем скачать другие рефераты по теме: шпаргалка рф, курсовая работа проблема.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата