Claw.ru | Рефераты по информатике, программированию | Двоичные деревья поиска Двоичные деревья поиска | Категория реферата: Рефераты по информатике, программированию | Теги реферата: отчет о прохождении практики, шпоры на экзамен | Добавил(а) на сайт: Dvoreckov. Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата 37         node = node.nodeParent.nodeParent; 38       End 39       Else 40       Begin 41         If (node == node.nodeParent.left) Then 42         Begin 43           node = node.nodeParent; 44           RBTRightRorate(Tree,node); 45         End 46         node.nodeParent.color = BLACK; 47         node.nodeParent.nodeParent.color = RED; 48         RBTLeftRotate(Tree,node.nodeParent.nodeParent); 49       End 50     End 51   End 52   Tree.root.color = BLACK; 53 End

Функция RBTInsert не так сложна, как кажется на первый взгляд. Рассмотрим её подробнее. После строк 3-4 выполняются все свойства КЧД, кроме, возможно, одного: у новой красной вершины может быть красный родитель. Такая ситуация (красная вершина имеет красного родителя) может сохраниться после любого числа итераций цикла. Внутри цикла рассматриваются 6 различных случаев, но три из них (строки 8-28) симметричны трём другим (строки 30-50), различие лишь в том, является ли родитель вершины node правым или левым потомком своего родителя (случаи разделяются в строке 7). Поэтому мы рассмотрим подробно только первые три случая (строки 8-28). Предположим, что во всех рассматриваемых КЧД корень чёрный, и будем поддерживать это свойство (строка 52). Поэтому в строке 5 node.nodeParent (красного цвета) не может быть корнем, и node.nodeParent.nodeParent != NIL. Операции внутри цикла начинаются с нахождения nodeTemp, “дяди” node, то есть вершины, имеющей того же родителя, что и node.nodeParent. Если nodeTemp – красная вершина, то имеет место случай 1, если черная, то 2 или 3. Во всех случаях вершина node.nodeParent.nodeParent – чёрная, так как пара node, node.nodeParent была единственным нарушением свойств КЧД.

Случай 1 (строки 12-15 и 34-37) показан на рисунке 6. Является ли вершина node правым или левым потомком своего родителя, значения не имеет.

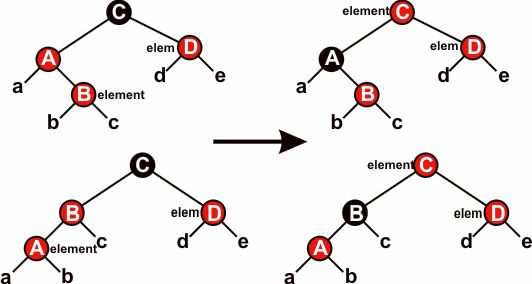
Рисунок 6.

Обе вершины (node и nodeTemp) – красные, а вершина node.nodeParent.nodeParent – чёрная. Перекрасим node.nodeParent и nodeTemp в чёрный цвет, а node.nodeParent.nodeParent – в красный. При этом число чёрных вершин на любом пути от корня к листьям остаётся прежним. Нарушение свойств КЧД возможно лишь в одном месте: вершина node.nodeParent.nodeParent может иметь красного родителя, поэтому надо продолжить выполнение цикла, присвоив node значение node.nodeParent.nodeParent.

В случаях 2 и 3 вершина nodeTemp – чёрная. Различаются случаи, когда вершина node является правым или левым потомком своего родителя. Если правым, то это случай 2 (строки 20-23 и 41-45). В этом случае производится левое вращение, которое сводит случай 2 к случаю 3, когда node является левым потомком своего родителя. Так как node и node.nodeParent – красные, после вращения количество чёрных вершин на путях от корня к листьям остается прежним.

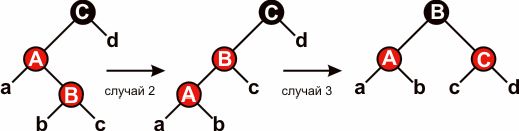
Рисунок 7.