Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



(2.4)

Различают два вида компонент, общие и генеральные. Генеральные главные компоненты существенно связаны со всеми признаками задачи, общие - более чем с одним.

Несмотря на то, что вместо признаков получено такое же количество главных компонент, вклад в общую дисперсию большинства оказывается небольшим. Можно исключить из рассмотрения те компоненты, вклад которых мал.

Итак, при проведении эксперимента мы получаем результаты в виде матрицы наблюдаемых величин ХN,n где N - число наблюдаемых объектов, n - число измеряемых признаков.

Элементы данной матрицы центрируются и нормируются, и мы получаем матрицу Y.

Выясним, что представляют собой весовые коэффициенты между признаками и главными компонентами. Для этого умножим на первую главную компоненту и получим:

. (2.5)

Чтобы получит коэффициент корреляции между j-ым признаком и первой главной компонентой, просуммируем левую часть по всем N наблюдениям и разделим сумму на число наблюдений N, тогда правая часть примет вид:

. (2.6)

Учитывая, что , перепишем выражение:

, (2.7)

где -коэффициент корреляции между j-ым признаком и r-й главной компонентой, - коэффициент корреляции между r-й и первой главной компонентой, - весовые коэффициенты, которые называются в факторном анализе коэффициентами отображения. Поскольку в методе главных компонент компоненты не коррелированны между собой, можно записать =0 (r¹ k), поэтому =. И в общем случае в методе главных компонент можно написать =.

Матрица наблюденных коэффициентов корреляции может быть представлена так:

R=YY¢ , (2.8)

где Y - матрица нормированных значений признаков, Y¢ - транспонированная матрица.

Коэффициент корреляции характеризует связь между двумя случайными величинами Хj и Хr в случае линейной корреляции между ними. Коэффициент корреляции представляет эмпирический первый основной смешанный момент. Для любых признаков и случайных величин , (2.9)

Среднее значение случайной величины Хj определяется по формуле

, (2.10)

а среднеквадратическое отклонение

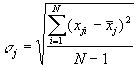. (2.11)

В результате преобразований корреляционной матрицы можно получить y=UL 1/2f, где L -матрица собственных значений матрицы R, U - матрица из собственных векторов R. Отсюда можно заключить, что искомая матрица А может быть определена как А=UL 1/2, или, соответственно для столбцов .

2.2.2. Геометрическая интерпретация метода главных компонент

Геометрической интерпретацией метода главных компонент служит переход к новой системе координат, где осями служат главные компоненты распределения. [3,11].

Рассмотрим простейший двумерный случай. Она представлена на Рис 2.1.

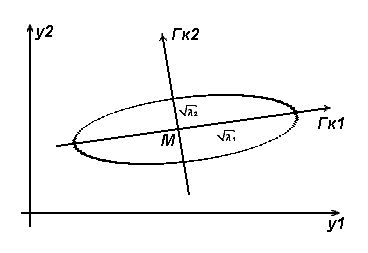
Рис. 2.1. Геометрическая интерпретация метода главных компоент для двумерного случая

2.2.3 Блок схема алгоритма

Блок схема алгоритма метода главных компонент приведена на рисунке 2.2.

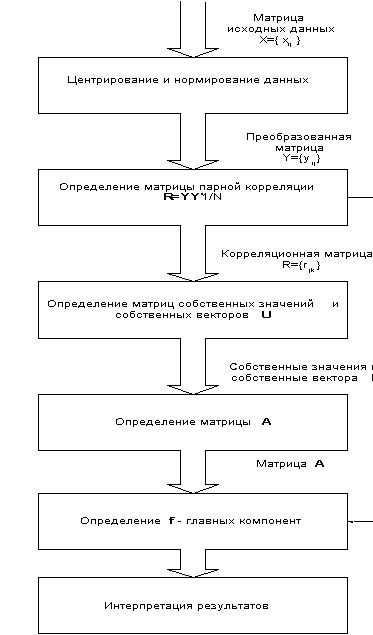
Рис 2.2. Блок схема алгоритма метода главных компонент

2.2.4 Обратная факторная задача

Как было указано выше, каждая главная компонента даёт некую новую общую характеристику всем изучаемым объектам. Причем каждая компонента является функцией особенностей каждого из изучаемых объектов. Часто нас интересует случай, когда нас интересуют качества объектов, связанные с одной или несколькими главными компонентами. Если было бы возможно получить значение компоненты для каждого из рассматриваемых пациентов, то их можно было бы ранжировать и классифицировать по такой важной интегральной особенности, как тяжесть ранения.

Обратимся к модели метода главных компонент. Развернём равенство , для j-ого признака:

(2.13)

Выразим теперь значения главных компонент через значения признаков. Для r-ой компоненты:

. (2.14)

Предложенный метод не является единственным, зато он легко программируется на ЭВМ.

2.2.5 Проблема собственных чисел и собственных значений

При решении задачи методом главных компонент возникает проблема вычисления собственных чисел и собственных векторов. В соответствующей литературе, посвященной методу главных компонент [4], для решения этой проблемы рекомендуется воспользоваться стандартными подпрограммами и библиотеками, входящими в поставку программного обеспечения ЭВМ. Однако, в связи с грандиозным прогрессом в области вычислительной техники, развитием персональных ЭВМ, и переориентацией рынка программных средств, данные рекомендации теряют актуальность. Очевидно так же, что и при написании этой методической литературы, данные рекомендации не являлись идеальными, так как при использовании стандартных подпрограмм никак не используются свойства матриц, получающихся при расчетах методом главных компонент.

2.2.6 Методы нахождения собственных чисел и собственных векторов

2.2.6.1 Постановка задачи

Собственным значением квадратной матрицы А называется такое число l , что для некоторого ненулевого вектора х имеет место равенство Ах=l х. Любой ненулевой вектор х, удовлетворяющий этому равенству, называется собственным вектором матрицы А, соответствующим собственному значению l . Все собственные векторы матрицы определены с точностью до числового множителя. Множество всех собственных значений матрицы А называется спектром матрицы А.

Собственные значения l матрицы А являются корнями алгебраического уравнения:

(2.16)

которое называется характеристическим уравнением матрицы А.

Известно, что характеристическое уравнение имеет в области комплексных чисел ровно m корней l 1, l 2, ..., l m (с учетом их кратности). Таким образом каждая квадратная матрица А порядка m обладает набором из m собственных значений l 1, l 2, ..., l m.

Если матрица А симметричная, то все её собственные значения являются вещественными числами. В противном случае, для несимметричных матриц возможно наличие комплексных собственных значений вида l =a + ib с ненулевой мнимой частью. В этом случае собственным значением матрицы будет и комплексно-сопряженное число.

Рекомендуем скачать другие рефераты по теме: россия диплом, государство реферат.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата