Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата



Численные методы решения проблемы собственных значений до конца 40-х годов, сводились, в основном, к решению характеристического уравнения. При реализации такого подхода, основные усилия были направлены на разработку эффективных методов быстрого вычисления коэффициентов характеристического уравнения. Такие методы имеют названия прямых. Популярным методом этого типа является метод Данилевского [10].

Указанный подход становится неудовлетворительным при вычислении собственных значений матриц, имеющих порядок m в несколько десятков (и тем более сотен). В частности, одним из недостатков является так же то, что точность вычисления корней многочлена высокой степени данным методом чрезвычайно чувствительна к погрешности в коэффициентах, и на этапе вычисления последних может быть в значительной степени потеряна информация о собственных значениях матрицы.

С появлением ЭВМ широкое распространение получили интерполяционные методы решения проблемы собственных значений, не использующие вычисление характеристического многочлена. В настоящее время эти методы почти полностью вытеснили прямые.

2.2.6.2 QR разложение матрицы

В настоящее время лучшими методами вычисления всех собственных значений квадратных заполненных матриц общего вида являются алгоритмы, основанные на QR разложении, которое позволяет получить представление исходной матрицы А в виде произведения ортогональной матрицы Q на верхнюю треугольную матрицу R. Планарные (плоские) вращения (они же вращения Якоби или Гивенса) представляют собой наиболее простое средство получения искомого ортогонального разложения. Метод планарных вращений может быть естественным образом обобщен для получения более удобных форм ортогональных вращений, осуществляемых в пространстве с произвольным числом измерений. Такими обобщениями является алгоритм Хаусхольдера (метод отражений) и модифицированный алгоритм Грама - Шмидта [1,8].

Очевидно, что для полного разложения, независимо от применяемого алгоритма, требуется некая последовательность ортогональных преобразований, которые могут быть представлены матрицами Q0,Q1,...,Qm. Таким образом, полученная в результате матрица примет вид Q= Q0,Q1,...,Qm.

2.2.6.3 Метод вращений ( метод Гивенса)

Отдельное планарное вращение, применяемое к матрице А, эквивалентно умножению её на матрицу вида:

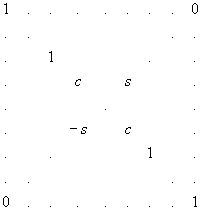(2.15)

где с=cosq , s=sinq , q - угол вращения. Таким образом, в процессе преобразования матрицы изменяются только её элементы строк i и l.

Предположим, что в результате проведенных преобразований расположенные ниже главной диагонали элементы строк с 1 по l матрицы А стали равными нулю. Тогда для обращения в нуль расположенных ниже главной диагонали элементов (l+1) -й строки матрицы А осуществляется её вращение последовательно с первой, второй и последующими строками. Этот процесс продолжается до тех пор, пока все расположенные ниже главной диагонали элементы (l+1) -й строки не станут равными нулю. То есть, пока не получим треугольную матрицу вида:

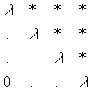(2.16)

Назовём полученную матрицу матрицей R, она связана с исходной матрицей равенством R=ТА, где Т=Тm-1,m...T

2.2.6.4 Метод Якоби

Метод Якоби является частным случаем метода Гивенса, для симметрической матрицы А, следовательно вычисление всех собственных значений и собственных векторов вещественной симметрической матрицы можно свести к отысканию такой ортогональной матрицы Т, для которой произведение D = ТTАT представляет диагональную матрицу, причем столбцы матрицы Т будут являться соответствующими собственными векторами матрицы А. Матрица Т находится как предел бесконечного произведения элементарных матриц вращений, каждая из которых имеет вид

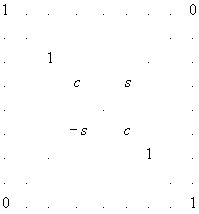(2.17)

где с=cosj , s=sinj , j - угол вращения.

Если необходимо обратить в нуль аik матрицы А, то соsj и sinj нужно выбрать по формулам

,

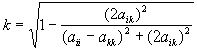, (2.18)

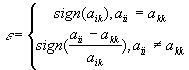
Тогда получим матрицу D = ТTmATm с измененными i-м и k-м столбцами и строками:

bii=cos2j aii+sin2j akk+2cosj sinj aik,

bkk=sin2j aii+cos2j akk- 2cosj sinj aik,

bik=bki=0, (2.19)

bij=bji=cosj aji+sinj ajk

bkj=bjk=sinj aji- sinj ajk

j=1,...n, j¹ i, j¹ k,

bji=aji,

в остальных случаях.

Отметим, что выполняется соотношение b2ii+b2kk=a2ii+a2kk+2a2ik, т.е. сумма квадратов диагональных элементов увеличивается.

Соответственно на ту же величину уменьшается сумма квадратов внедиагональных элементов, откуда и следует сходимость к диагональной матрице. Элементы, которые однажды обратились в нуль, при последующих шагах снова могут стать ненулевыми.

2.2.6.5 Приведение матрицы собственных чисел к виду необходимому для метода главных компонент

Для метода главных компонент необходимо, чтобы собственные число были расположены в порядке убывания. Матрица собственных чисел, получающаяся в методе Якоби, не выполняет данное требование. Для получения искомой матрицы переставим строки в матрицах L и А (помним что L =ТА) так чтобы max{l } было в первом столбце, получив соответственно матрицы L * и А*. Теперь для того чтобы матрица L * опять стала диагональной требуется применить планарное вращение Тij (где i,j переставленные строки). Получаем L *= ТijТА*.

Применяя подобные перестановки и планарные вращения далее, легко получить требуемую матрицу, у которой |l 1|>|l 2|>...|l m|.

2.2.6.6. Алгоритм метода Якоби

Блок схема алгоритма метода Якоби приведена на Рис. 2.3.

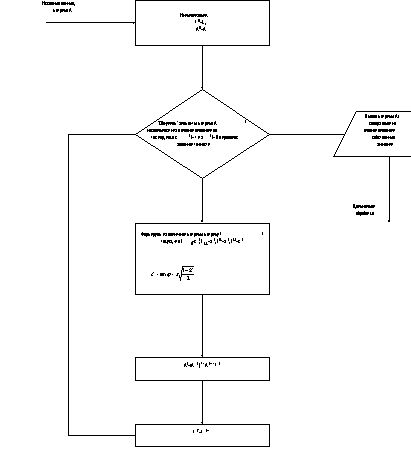
Рис. 2.3. Блок схема алгоритма метода Якоби

2.2.7. Применение метода главных компонент в задаче оценки эффективности функционирования военно-медицинского учреждения

Исходные данные для анализа представляют собой таблицу собранных статистических данных, объектами в которой являются отделения ГВКГ, а параметрами - установленные ГВМУ показатели для оценки эффективности использования коечного фонда (Таблица 2.1).

В методических рекомендациях Министерства здравоохранения РФ даются следующие статистические показатели использования коечного фонда госпиталя (лечебного отделения):

1. Среднее число развернутых коек:

.

Рекомендуем скачать другие рефераты по теме: россия диплом, государство реферат.

Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата