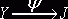
следует
рассматривать как интерпретацию обработанных сообщений Y. Здесь множество J
есть также множество пар смысл-значение.
Представление
обработки в форме (3.2), хотя и не охватывает всех видов обработки сообщений, тем не менее является достаточно общим, чтобы рассматривать многие виды
обработки сообщений в технических системах.
Принимая
во внимание правило обработки (3.2) и правила интерпретации (3.1) и (3.3), получаем следующую зависимость отображений j, y и q:
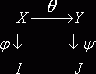
Из
диаграммы видно, что каждому сообщению xÎX поставлен в
соответствие ровно один образ j(x)ÎI и ровно один образ y(q(x))ÎJ. Действительно:
yÎY
имеет образ y(y)ÎJ;
xÎX
имеет образ q(x)ÎY, [q(x)=y];
xÎX
имеет образ y(q(x)).
Учитывая
это, на множествах I, J можно определить отношение h, которое может выражать
такой смысл: иметь общий прообраз во множестве X. Данное отношение h не
обязательно является отображением. Так, если отображение j не
биективно, то элемент множества I может иметь более одного прообраза во
множестве X. Каждый прообраз как элемент множества X имеет по одному образу в
множестве J, и, следовательно, рассматриваемый элемент из множества I находится
в отношении h
с числом элементов из множества J, равным числу его прообразов в множестве X. В
силу этого отношение h не является отображением.
Правило
обработки j
сообщения X называется сохраняющим информацию, если отношение h
является отображением, а диаграмма (3.4) принимает вид
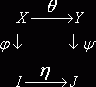
Из
диаграммы следует, что произведение отношения jh равно произведению qy, т.
е. диаграмма (3.4) является коммутативной. Определяющим отображением в
диаграмме (3.4) является отображение h – правило обработки
информации. Поэтому названия различных видов обработки сообщений происходят из
смысла и имени правила h. Обычно при выборе вида обработки сообщений исходят из
правила h
с учетом правил интерпретации сообщений j и y.
Пусть
q
и h
– взаимно однозначные отображения. Это относится к случаю, когда к правилу q
предъявляется требование не терять информацию в процессе обработки, например
при перемене носителя информации, переходе от одного вида модуляции к другому и
т. и.
Рассмотрим
пример из области сообщений на естественном языке. Очевидно, сообщение «ЭВМ
облад. сп-стью обр-ки инф-ии», благодаря избыточности текста на естественном
языке однозначно восстанавливается как «ЭВМ обладает способностью обработки
информации».
В
рассмотренных примерах существует обратное преобразование q-1, которое является однозначным, – позволяет восстановить исходный элемент xÎX
по известному yÎY, т. е. исходное сообщение по обработанному.
Рассмотрим
теперь случай, когда h является взаимно однозначным отображением, т.е.
интерпретация исходного сообщения может быть произведена точно, а q
взаимно однозначным отображением не является. Это значит, что множество X имеет
большее число элементов, чем множество Y. Тогда q есть сжимающее
отображение. В этом случае правило преобразования называется сжатием
информации, хотя правильнее говорить о сжатии сообщения или сжатии сигнала.
Наконец, если отображение h
не инъективно, то отображение q также не является взаимно однозначным. При этом
происходит потеря части информации в обработанном сообщении yÎY
по сравнению с той, которая содержится в исходном сообщении xÎX.
Существует много видов обработки информации.
Задачи обнаружения сигнала
Сигнал
s(t) распространяясь по каналу связи, искажается помехой, так что можно
говорить о том, что на вход приемника приходит не сигнал s(t), а другой сигнал x(t).
В
приемнике содержатся априорные сведения о сигнале:
1)
известен вид функции s(t) и известно, что она не равна нулю на интервале
времени (tн,tк),
2)
известна статистика помехи (например, плотность вероятности ее амплитуды).
В
приемнике решается, был ли передай сигнал на интервале времени (tн,tк) или нет.
Очевидно, что решение нельзя принять до наступления момента времени tн, а в
ряде случаев – и до наступления момента tк. Приемник анализирует сигнал x(t)
на интервале (tн,tк) и в некоторый момент времени t0³tк должен выдать
решение.
Рекомендуем скачать другие рефераты по теме: вид дипломной работы, классы реферат.
Предыдущая страница реферата |
1
2
3
4
5 |
Следующая страница реферата

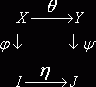
 Главная
Главная