Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Рассмотрим решение данной задачи при следующих ограничениях (условиях):

1) известен вид сигнала s(t), действующего в интервале времени (0, t0);

2) помеха n(t) является аддитивной и представляет собой белый шум, т.е. спектральная плотность мощности помехи Gn(f)=C, где – постоянная величина.

Приемник является линейной системой, к которой применим принцип суперпозиции. На вход приемника поступает воздействие, представляющее собой смесь полезного сигнала s(t) и помехи n(t): x(t)=s(t)+n(t).

Реакцию такой системы на это входное воздействие можно представить как сумму p(t)=x(t)+e(t), где x(t) – реакция системы, вызванная воздействием полезного сигнала s(t); e(t) – результат преобразования системой помехи n(t). Такое разделение произвести можно, если приемник – линейная система.

Помеху, действующую в канале связи, практически нельзя уменьшить, поэтому для повышения помехоустойчивости и пропускной способности канала связи стремятся обычно увеличить мощность полезного сигнала s(t). Как правило, выбирают максимально возможную мощность, учитывая ограничения, накладываемые аппаратурой и самой линией связи, чтобы обеспечить максимальное отношение Pc/sn2, где Pc – мощность полезного сигнала, а sn2 – мощность помехи, отнесенные к входу приемника

Функция приемника – обработать сигнал, чтобы еще больше увеличить отношение сигнал/помеха. Рассмотрим задачу обнаружения сигнала на фоне помех как задачу синтеза линейного фильтра, на выходе которого в момент времени t0 имеет место максимум отношении x(t0)/se2, где se2 – мощность (дисперсия) помехи на выходе фильтра.

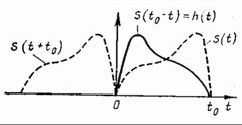
Рис. 3.1. Импульсная характеристика линейного фильтра

(3.6)

Синтез фильтра заключается в нахождении либо его частотной характеристики W(jf), либо его импульсной характеристики h(t). При этом необходимо, чтобы выполнялось условие

min[-2kx(t0)],

где k – произвольный постоянный коэффициент.

Учитывая, что спектр помехи e(t) на выходе фильтра зависит от его частотной характеристики:

,

определим мощность помехи:

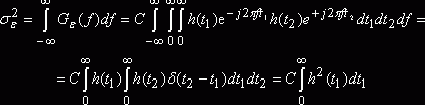
Выходной сигнал фильтра в момент времени t0

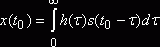
Преобразуем выражение (3.6):

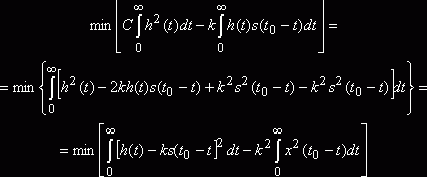
Интеграл 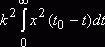 представляет собой энергию сигнала и при заданной функции s(t) является постоянной величиной. Условием минимума является равенство нулю интеграла 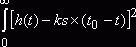, т.е. .

Это условие эквивалентно равенству , означающему, что наибольшее отношение сигнал/помеха в момент времени t0 на выходе фильтра достигается тогда, когда импульсная характеристика фильтра является зеркальным отображением полезного сигнала s(t+t0) (рис. 3.1).

Сжатие и адаптивная дискретизация сигналов

Рассмотрим источники измерительной информации и измерительные сигналы. В качестве источников измерительной информации выступают физические объекты разнообразной природы. Для отбора измерительной информации используются различные измерительные преобразователи, основная функция которых состоит в превращении контролируемого параметра или параметров объекта измерения в сигналы. Поэтому ряд свойств измерительных сигналов определяются как видом объекта измерения, так и условиями измерения.

В измерительной технике актуальна проблема обработки больших потоков измерительной информации. Решая эту проблему, можно пойти двумя путями: увеличивать быстродействие средств обработки информации или же сократить объемы обрабатываемой информации.

Рекомендуем скачать другие рефераты по теме: вид дипломной работы, классы реферат.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата