Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата



Под надежностью понимают свойство изделия выполнять заданные функции, сохранять свои эксплутационные показатели в заданных пределах в течении требуемого промежутка времени или требуемой наработки при соблюдении режимов эксплуатации, правил обслуживания, хранения и т.д.

Надежность не может быть измерена непосредственно как любая физическая величина. Она может быть только количественно оценена или предсказана. Для оценки основных показателей надежности используют математический аппарат теории вероятности

Показатели надежности неремонтируемых систем. Неремонтируемые системы работают до первого отказа после чего заменяются новыми. Все количественные показатели надежности неремонтируемых систем являются общими и выражаются одними и теми же математическими зависимостями, но их конкретные числовые значения зависят от режимов работы изучаемых систем.

Показатели надежности неремонтируемых систем базируются на понятиях функций надежности Р(t) и функции отказа Q(t), связанных зависимостью P(t) = 1- Q(t). Обе они зависят от времени t.

Вероятностью безотказной работы P(t) называют вероятность того, что в заданном интервале времени или пределах заданной наработки ti отказов в системе не возникает, т.е. P(ti) = P(T>ti), где Т - случайная величина характеризующая время наработки системы до возникновения в ней отказа. Соответственно вероятностью возникновения отказа в системе Q(ti) называется вероятность того, что в период наработки ti в ней обязательно произойдет отказ, т.е. Q(ti) = P(T< ti).

Теоретическое значение вероятности безотказной работы ЭВА удобно определить следующим образом :

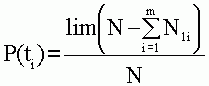(4.1),

где

N1i - число изделий, отказавших во время испытаний на i-том интервале времени;

m = t / 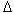t - число интервалов

t - время испытания

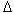t - продолжительность интервала времени

По аналогии с (4.1) статистическая вероятность безотказной работы ЭВА

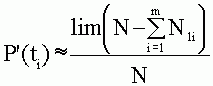(4.2),

Естественно, чем больше N, тем более точно соблюдается равенства, и тем точнее становятся значения величин P(ti) и P’(ti).

Вероятность безотказной работы может быть определена и для произвольного интервала времени (t1 ; t2), т.е. не с момента включения системы. В этом случае говорят об условной вероятности безотказной работы системы P(t1 ; t2) в период (t1 ; t2), имея в ввиду, что в момент времени t1 система находится в работоспособном состоянии. Условная вероятность P(t1 ; t2) определяется соотношением

P(t1 ; t2) = P(t2) / P(t1) (4.3)

где

P(t1) и P(t2) - соответственно значения функций надежности в начале и конце наработки.

Плотностью распределения наработки до отказа f(t) называют производную по времени от функции отказа Q(t):

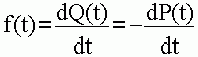(4.4)

Из (4.4) следует, что величина f(t)dt характеризует безусловную вероятность того, что система обязательно откажет в интервале времени (t ; t+dt) при условии что в момент времени t она находилась в работоспособном состоянии.

Наиболее распространенным показателем надежности является интенсивность отказов. Интенсивность отказов 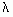(t) представляет собой условную вероятность возникновения отказа в системе в некоторый момент времени наработки при условии, что до этого момента отказов в системе не было. Величина интенсивности определяется отношением: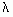(t) = f(t)/ P(t). Приблизительно ее можно оценить следующим отношением :

,

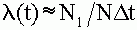где

N1 - число изделий, отказавших при испытаниях в течении времени 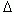t

N - число изделий, работоспособных к началу испытаний.

Условная работоспособность системы в момент начала наработки можно записать в виде P(0) = 1. Тогда из (4.3) и (4.4) следует что

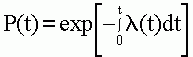
Аналогично может быть определена условная вероятность

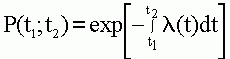
Таким образом мы рассмотрели три показателя надежности. Очевидно, что достаточно знать одну (любую) из них, чтобы определить два других. Таким образом все три показателя являются равноправными. Однако в большинстве случаев предпочтение отдают интенсивности отказов.

В качестве показателя надежности используют среднюю наработку до отказа tcp. Средняя наработка до отказа представляет собой математическое ожидание M(t) случайной величины t

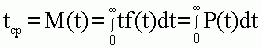
Вид функций f (t) и P (t) определяется конкретными законами распределения случайной величины t. Средняя наработка до отказа - это ожидаемое время исправной работы системы до первого отказа. Приближенно ее можно оценить так:

,

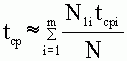где

tcp i = (ti - ti-1) / 2

(ti ; ti-1) - время в начале и конце i-того интервала.

Таким образом мы рассмотрели основные показатели надежности систем./ 4 /

4.2. Методика расчета надежности

Рекомендуем скачать другие рефераты по теме: курсовые, архитектура реферат.

Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата