Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата



Пусть Sn(Mi) – сеансовый ключ, вычисленный каждым Mi. Для 0<i<n-1  можно записать его как aCiriK-1in. Для Mn Sn(Mn)=aCnrn, где ci возможно известно противнику C. C также знает подмножество {aП(S)| SÌ{r1,…,rn}}. В данных условиях нахождение aKin или aK-1in невозможно, если вычислительно трудно решить проблему “распознавания Диффи-Хеллмана” [1].

Однако, некоторые из атак возможны. Если С попытается послать M1 некоторое  ac1 на последнем этапе протокола (где с1 выбирается противником), то M1 в результате получит неверный ключ Sn(M1)=ac1r1K-11n, обнаружит проблему и просто заново запустит протокол обмена. Допустим, что противник каким-то образом получил этот неверный ключ (заметим, что на практике это маловероятно). При повторном выполнении протокола С может подменить сообщение от Mn-1  к Mn  на

ac1r1K1n-1,…,ac1r1.

С подменил первое и последнее слово в сообщении, остальные слова не изменялись. Тогда Mn вычислит ключ Sn(Mn)=(ac1r1)rn. Mn также вычислит

(ac1r1K1n-1)rnK1n=ac1r1rn

и отошлет это значение M1 в последнем этапе протокола. В результате С будет знать ключ M1. Но (хотя в работе [1] это и не отмечается), общий групповой ключ опять не совпадет, и через некоторое время протокол придется повторить снова. Все дело во времени определения конфликта ключей. Однако, в такого типа атаке очень много условностей, и поэтому ее можно отнести к разряду теоретических, а не к реально осуществимым атакам. Кроме того, как указано в [1], простым средством предотвращения таких атак является вычисление в качестве ключа Sn=h(Sn(Mi ), где h() – любая хеш-функция.

Необходимо заметить, что вышеупомянутый протокол A-GDH.2 выполняет неявную аутентификацию ключа, причем в довольно слабой форме, поскольку ключ не аутентифицируется непосредственно между каждыми любыми двумя Mi и Mj участниками (i¹j). Последний участник Mn (будем далее называть его контролирующим группы, поскольку через него проводятся ключевые операции протокола) отвечает за использование аутентичных ключей Kin, i=1 ... n-1, от которых и зависит аутентификация. Следовательно, участник Mn должен быть лицом, которому все доверяют. Это может быть схема с доверенным сервером в качестве Mn. В противном случае Mn сможет разбить группу на две части без обнаружения этого (поскольку он может перехватывать все сообщения и таким образом получить необходимую информацию в виде     a r1…ri / rj для "i,j).

Поэтому необходимо трансформировать протокол, что и было сделано в работе [1].

2.2 Протокол SA-GDH.2

Для описания протокола требуется несколько дополнительных определений.

Опр. 2.2.1. Пусть R – протокол обмена для n участников и M – множество участников. Мы будем говорить, что  R является протоколом, обеспечивающим полную(complete) аутентификацию группового  ключа, если для каждых  i,j (0< i¹j £n) участники Mi и Mj вычислят общий ключ Si,j, только если Si,j был получен при участии каждого Mp Ì M.

Другими словами, полная аутентификация группового ключа есть аутентичный обмен для выработки ключа между всеми парами (Mi, Mj) при (0< i¹j £n).

Для выполнения этого определения можно модифицировать протокол A-GDH.2 в следующий:

Протокол SA-GDH.2. Этап i (0< i <n): 1. Mi  (i-1) . 2.  Mi  обновляет каждое Vk следующим образом:               (Vk ) riK ik = a (r1…ri / rk)(K k1…K ki)   при  k < i Vk =       (Vk ) riK ik = a (r1…ri)(K k1…K ki)       при k > i    .               Vk                                              при k = i (Замечание: на первом этапе M1 выбирает V1 = a .) Этап n: 1. Mn рассылает множество всех Vk участникам группы. 2. При получении Mi выбирает свое Vi =a (r1…rn / ri)(K1i…K ni). Mi вычисляет (Vk ) ri(K1i-1… K ni-1)= a r1…rn . Заметим, что вместо того, чтобы вычислять n обратных элементов, Mi может вычислять 1 обратный элемент Pi-1=(K1i-1… Kni-1), где Pi=(K1i… Kni).

В протоколе SA-GDH.2 требуется, чтобы каждый участник группы имел некоторый общий ключ с любым другим участником (это значение Kji). Однако, как уже было замечено для каждого такого ключа Kji не требуется нахождение обратного Kji-1. Таким образом, достаточно получить такие ключи перед началом работы в группе и затем эти ключи могут оставаться постоянными, не добавляя лишних действий в протокол.

Протокол основан на кольцевой схеме взаимодействия, т.е. данные проходят по кругу и лишь на последнем этапе идет широковещательная рассылка. Данные, которые передаются, представляют собой множество из n элементов. i-й  элемент содержит своеобразное «накопление ключа» для i-го участника. Во время обновления ключа каждый из участников вносит свой вклад в формирование ключа. Только пройдя полный круг, i-й элемент множества будет иметь вклады  всех участников и их секретные ключи для связи с i-м абонентом (рис. 1). Это позволяет избежать явной замены противником одного из значений на какое-то другое, выгодное ему (возможное вмешательство противника рассмотрим далее)

Однако SA-GDH.2 имеет более высокую «вычислительную стоимость» по сравнению с A-GDH.2. Прежде всего, он требует (n-1) экспоненцирование для каждого Mi (кроме первого), в отличие от i экспоненцирований в A-GDH.2. К этому еще добавляется работа по формированию общих ключей для каждой пары абонентов (если они не вычислены заранее): на последнем этапе проводится одно экспоненцирование – как и в A-GDH.2. На рис. 1 приведены примеры протоколов A-GDH.2 и SA-GDH.2.

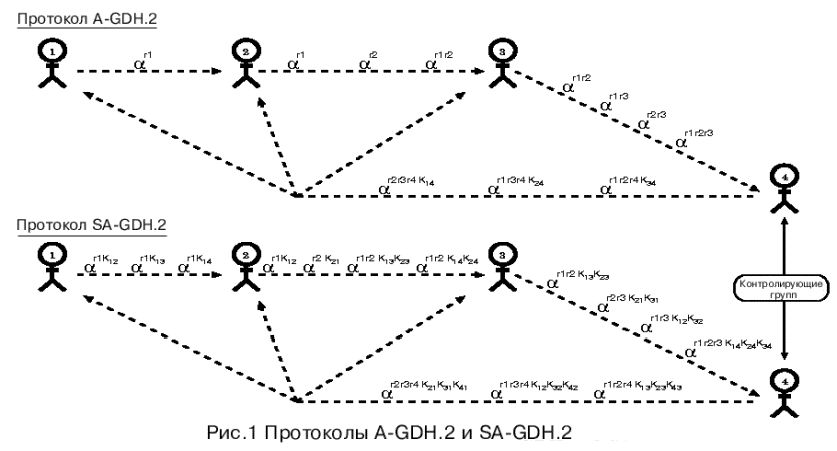
Как показано в [1], протокол SA-GDH.2 обеспечивает полную аутентификацию группового  ключа.

 Теорема 2.2.1 Протокол SA-DH обеспечивает полную аутентификацию группового  ключа.

Док-во: предположим, Mi и Mj вычислили одинаковый ключ в результате выполнения протокола. Пусть Kn=Sn(Mi)=Sn(Mj), и предположим, что некто Mp ÎM (p¹i,j) не сделал вклада в этот ключ. Пусть Vi и Vj обозначают величины, полученные Mi и Mj на последнем этапе протокола. Напомним, что в соответствии с протоколом

Sn(Mi)=(Vi)(K1i-1…Kni-1)ri и Sn(Mj)=(Vj)(K1j-1…Knj-1)rj .

Поскольку все участники группы сделали вклад в ключ, то можно записать, что

 

Vi=a (r1…rn/rpri)(K1i-1…Kni-1/Kpi-1) (для Vj аналогично), и

Sn(Mi)= a (r1…rn/rp)Kpi-1, что должно равняться Sn(Mj)= a (r1…rn/rp)Kpj-1.

Но поскольку Kpi-1 и Kpj-1 являются секретными, то получаем противоречие. #

В работе [1] также отмечается, что обсуждаемый протокол обладает устойчивостью к атакам по известному ключу (known key attacks), однако строгого формального доказательства не приведено, авторы лишь отмечают, что это легко пронаблюдать на приведенной выше атаке на A-GDH.2.

2.3 Особенности ключей протоколов A-GDH.2 и SA-GDH.2

Рассмотрим важное свойство протоколов – а именно подтверждение ключа. Не для каждого протокола это свойство является необходимым: например, оно не нужно, если взаимодействие с полученным ключом происходит немедленно. Но тем не менее свойство подтверждения ключа является желательным для протоколов обмена по следующим причинам:

Рекомендуем скачать другие рефераты по теме: решебник по химии, реферат методы.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата