Claw.ru | Рефераты по информатике, программированию | Сортировка данных в массиве Сортировка данных в массиве | Категория реферата: Рефераты по информатике, программированию | Теги реферата: сочинение рассуждение, реферат молодежь | Добавил(а) на сайт: Funtusov. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата       j--;     }     // точка вставки найдена; вставить temp     A[j] = temp;   } }

Вычислительная эффективность сортировки вставками

Сортировка вставками требует фиксированного числа проходов. На n-1 проходах вставляются элементы от A[1] до A[n-1]. На i-ом проходе вставки производятся в подсписок A[0]–A[i] и требуют в среднем i/2 сравнений. Общее число сравнений равно

1/2 + 2/2 + 3/2 + ... + (n-2)/2 + (n-1)/2 = n(n-1)/4

В отличие от других методов, сортировка вставками не использует обмены. Сложность алгоритма измеряется числом сравнений и равна O(n2). Наилучший случай – когда исходный список уже отсортирован. Тогда на i-ом проходе вставка производится в точке A[i], а общее число сравнений равно n-1, т.е. сложность составляет O(n). Наихудший случай возникает, когда список отсортирован по убыванию. Тогда каждая вставка происходит в точке A[0] и требует i сравнений. Общее число сравнений равно n(n-1)/2, т.е. сложность составляет O(n2).

В принципе, алгоритм сортировки вставками можно значительно ускорить. Для этого следует не сдвигать элементы по одному, как это продемонстрировано в приведенном выше примере, а находить нужный элемент с помощью бинарного поиска, описанного в предыдущем номере (то есть, в цикле разбивая список на две равные части, пока в списке не останется один-два элемента), а для сдвижки использовать функции копирования памяти. Такой подход дает довольно высокую производительность на небольших массивах. Основным узким местом в данном случае является само копирование памяти. Пока объем копируемых данных (около половины размера массива) соизмерим с размером кэша процессора 1 уровня, производительность этого метода довольно высока. Но из-за множественных непроизводительных повторов копирования, этот способ менее предпочтителен, чем метод «быстрой» сортировки, описанный в следующем разделе. Этот же метод можно рекомендовать в случае относительно статичного массива, в который изредка производится вставка одного-двух элементов.

«Быстрая» сортировка

Итак, мы рассмотрели алгоритм сортировки массива, имеющий сложность порядка O(n2). Алгоритмы, использующие деревья (турнирная сортировка, сортировка посредством поискового дерева), обеспечивают значительно лучшую производительность O(n log2n). Несмотря на то, что они требуют копирования массива в дерево и обратно, эти затраты покрываются за счет большей эффективности самой сортировки.

Широко используемый метод пирамидальной сортировки также обрабатывает массив «на месте» и имеет эффективность O(n log2n). Однако «быстрая» сортировка, которую изобрел К.Хоар, для большинства приложений превосходит пирамидальную сортировку и является самой быстрой из известных до сих пор.

Описание «быстрой» сортировки

Как и для большинства алгоритмов сортировки, методика «быстрой» сортировки взята из повседневного опыта. Чтобы отсортировать большую стопку алфавитных карточек по именам, можно разбить ее на две меньшие стопки относительно какой-нибудь буквы, например K. Все имена, меньшие или равные K, идут в одну стопку, а остальные – в другую.

 

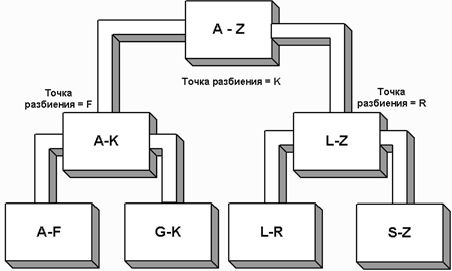
Рис.2

Затем каждая стопка снова делится на две. Например, на рисунке 2 точками разбиения являются буквы F и R. Процесс разбиения на все меньшие и меньшие стопки продолжается.

В алгоритме «быстрой» сортировки применяется метод разбиения с определением центрального элемента. Так как мы не можем позволить себе удовольствие разбрасывать стопки по всему столу, как при сортировке алфавитных карточек, элементы разбиваются на группы внутри массива. Рассмотрим алгоритм «быстрой» сортировки на примере, а затем обсудим технические детали. Пусть дан массив, состоящий из 10 целых чисел:

A = 800, 150, 300, 600, 550, 650, 400, 350, 450, 700

Фаза сканирования

Массив имеет нижнюю границу, равную 0 (low), и верхнюю границу, равную 9 (high). Его середина приходится на 4 элемент (mid). Первым центральным элементом является A[mid] = 550. Таким образом, все элементы массива A разбиваются на два подсписка: Sl и Sh. Меньший из них (Sl) будет содержать элементы, меньшие или равные центральному. Подсписок Sh будет содержать элементы большие, чем центральный. Поскольку заранее известно, что центральный элемент в конечном итоге будет последним в подсписке Sl, мы временно передвигаем его в начало массива, меняя местами с A[0] (A[low]). Это позволяет сканировать подсписок A[1]--A[9] с помощью двух индексов: scanUp и scanDown. Начальное значение scanUp соответствует индексу 1 (low+1). Эта переменная адресует элементы подсписка Sl. Переменная scanDown адресует элементы подсписка Sh и имеет начальное значение 9 (high). Целью прохода является определение элементов для каждого подсписка.

 

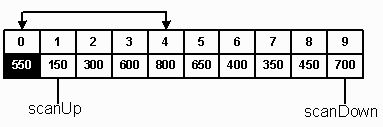
Рис.3

Оригинальность «быстрой» сортировки заключается во взаимодействии двух индексов в процессе сканирования списка. Индекс scanUp перемещается вверх по списку, а scanDown – вниз. Мы продвигаем scanUp вперед и ищем элемент A[scanUp] больший, чем центральный. В этом месте сканирование останавливается, и мы готовимся переместить найденный элемент в верхний подсписок. Перед тем, как это перемещение произойдет, мы продвигаем индекс scanDown вниз по списку и находим элемент, меньший или равный центральному. Таким образом, у нас есть два элемента, которые находятся не в тех подсписках, и их можно менять местами.

Swap (A[scanUp], A[scanDown]); // менять местами партнеров

Этот процесс продолжается до тех пор, пока scanUp и scanDown не зайдут друг за друга (scanUp = 6, scanDown = 5). В этот момент scanDown оказывается в подсписке, элементы которого меньше или равны центральному. Мы попали в точку разбиения двух списков и указали окончательную позицию для центрального элемента. В нашем примере поменялись местами числа 600 и 450, 800 и 350, 650 и 400 (см. рисунок 4).

 

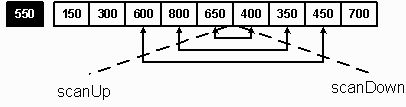
Рекомендуем скачать другие рефераты по теме: инвестиции реферат, реферат память.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата