Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Основная проблема и недостаток при использовании растровых изображений - это большие объемы данных. Для работ с большеразмерными иллюстрациями типа журнальной полосы требуются компьютеры с большими размерами оперативной памяти (128 Мбайт и более). Такие компьютеры, естественно, должны при этом иметь и высокопроизводительные процессоры.

Вторым недостатком растровых изображений является невозможность их увеличения для рассмотрения деталей. Так как изображение состоит из точек, то увеличение изображения приводит только к тому, что эти точки становятся крупнее. Никаких дополнительных деталей при увеличении растрового изображения рассмотреть не удается. Само увеличение точек растра визуально искажает иллюстрацию и делает ее грубой. Этот эффект называется пикселизацией.

Любое изображение, в том числе и трехмерное, состоит из графических примитивов, поэтому необходимо знать специальные методы генерации изображения, вычерчивание прямых и кривых линий, закраски многоугольников, создающей впечатление сплошных объектов. Рассмотрим некоторые из этих методов.

Алгоритмы вычерчивания отрезков. Экран дисплея можно рассматривать как матрицу дискретных элементов (пикселей), каждый из которых может быть подсвечен. В связи с этим нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселей, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пиксели труднее. Существует несколько алгоритмов выполняющих эту задачу, например, цифровой дифференциальный анализатор и алгоритм Брезенхема.

Алгоритм Брезенхема для генерации окружностей. В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т.е. окружностей, эллипсов, парабол, гипербол, посвящено значительное число работ. Наибольшее внимание уделено окружности. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит Брезенхему.

Вначале необходимо сгенерировать только одну восьмую часть окружности. Остальные ее части могут быть получены последовательными отражениями. Если сгенерирован первый октант (от 0° до 45° против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у = х, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой х = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = О для завершения построения.

Растровая развертка сплошных областей. Возможность представления сплошных областей в растровом графическом устройстве является его уникальной характеристикой. Генерация сплошных областей из простых описаний ребер или вершин называется растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две широкие категории: растровая развертка и затравочное заполнение.

В методах растровой развертки пытаются определить в порядке сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно идут от "верха" многоугольника или контура к "низу".

В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно.

Растровая развертка многоугольников. Можно разработать эффективный метод растровой развертки многоугольников, если воспользоваться тем фактом, что соседние пиксели, вероятно, имеют одинаковые характеристики (кроме пикселов граничных ребер). Это свойство называется пространственной когерентностью.

Алгоритм с упорядоченным списком ребер. Используя эти методы, можно разработать эффективные алгоритмы растровой развертки сплошных областей, называемые алгоритмами с упорядоченным списком ребер. Эффективность этих алгоритмов зависит от эффективности сортировки.

Алгоритм заполнения по ребрам. Алгоритм, использующий список ребер и флаг, является двухшаговым. Первый шаг состоит в обрисовке контура, в результате чего на каждой сканирующей строке образуются пары ограничивающих пикселов. Второй шаг состоит в заполнении пикселов, расположенных между ограничивающими.

Алгоритмы заполнения с затравкой. В рассмотренных алгоритмах заполнение происходит в порядке сканирования. Иной подход используется в алгоритмах заполнения с затравкой. В них предполагается, что известен хотя бы один пиксель из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пиксели, принадлежащие внутренней области. Области могут быть либо внутренние, либо гранично-определенные. Если область относится к внутренне-определенным, то все пиксели, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пиксели, внешние по отношению к области, имеют другой цвет. Если область относится к гранично-определенным, то все пиксели на границе области имеют выделенное значение или цвет. Алгоритмы, заполняющие внутренне-определенные области, называются внутренне-за-полняющими, а алгоритмы для гранично-определенных областей - гранично-заполняющими.

1.3 Векторная графика

Как в растровой графике основным элементом изображения является точка, так в векторной графике основным элементом изображения является линия, при этом не важно, прямая это линия или кривая.

В растровой графике тоже существуют линии, но там они рассматриваются как комбинации точек. Для каждой точки линии в растровой графике отводится одна или несколько ячеек памяти (чем больше цветов могут иметь точки, тем больше ячеек им выделяется). Соответственно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде формулы, а точнее говоря, в виде нескольких параметров. Чтобы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.

Линия - это элементарный объект векторной графики. Все, что есть в векторной иллюстрации, состоит из линий. Простейшие объекты объединяются в более сложные, например, объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб еще более сложен: его можно рассматривать либо как двенадцать связанных линий, либо как шесть связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.

Объекты векторной графики хранятся в памяти в виде набора параметров, но надо помнить о том, что на экран все изображения все равно выводятся в виде точек. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изобра жении объекта, поэтому векторную графику иногда называют вычисляемой графикой. Аналогичные вычисления производятся и при выводе объектов на принтер.

Как и все объекты, линии имеют свойства. К этим свойствам относятся: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т.п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Простейшая линия, если она не замкнута, имеет две вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.

1.4 Алгоритмы вычерчивания отрезков

Поскольку экран растрового дисплея с электронно-лучевой трубкой (ЭЛТ) можно рассматривать как матрицу дискретных элементов (пикселов), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. В сочетании с процессом построчной визуализации изображения он известен как преобразование растровой развертки. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пикселы труднее, что показано на рис. 1.1.

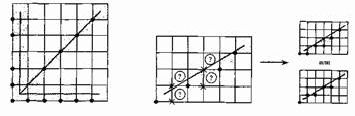
Рис. 1.1 Разложение в растр отрезков прямых

Прежде чем приступать к обсуждению конкретных алгоритмов рисования отрезков, полезно рассмотреть общие требования к таким алгоритмам и определить желаемые характеристики изображения. Очевидно, что отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках. Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона. Наконец, рисовать нужно быстро. Как это часто бывает, не все из перечисленных критериев могут быть полностью удовлетворены. Сама природа растрового дисплея исключает генерацию абсолютно прямых линий (кроме ряда специальных случаев), равно как и точное совпадение начала и конца отрезка с заданными точками. Тем не менее при достаточно высоком разрешении дисплея можно получить приемлемое изображение.

Постоянная вдоль всего отрезка яркость достигается лишь при проведении горизонтальных, вертикальных и наклоненных под углом 45 ° прямых. Для всех других ориентации разложение в растр приведет к неравномерной яркости, как это показано на рис. 2.1. Даже для частных случаев яркость зависит от наклона: заметим, например, что расстояние между центрами соседних пикселов для отрезка под углом 45° больше, чем для вертикальных и горизонтальных прямых. Поэтому вертикальные и горизонтальные отрезки будут выглядеть ярче, чем наклонные. Обеспечение одинаковой яркости вдоль отрезков разных длин и ориентации требует извлечения квадратного корня, а это замедлит вычисления. Обычным компромиссом является нахождение приближенной длины отрезка, сведение вычислений к минимуму, предпочтительное использование целой арифметики, а также реализация алгоритмов на аппаратном или микропрограммном уровне.

Рекомендуем скачать другие рефераты по теме: шпаргалка егэ, реферат на тему искусство.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата