Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата



В матричной форме это выглядит так:

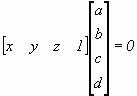
или

где представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.

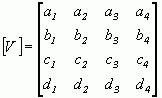
где каждый столбец содержит коэффициенты одной плоскости.

Напомним, что любая точка пространства представима в однородных координатах вектором

Более того, если точка [S] лежит на плоскости, то [S]*[P]T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают положительное скалярное произведение.

Хотя уравнение плоскости (3.1) содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d = 1 следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек (x1, y1, z1), (x2, y2, z2), (x2, y2, z2) в нормированное уравнение (3.1) дает:

ax1 + by1 + cz1 = - 1

ax2 + by2 + cz2 = - 1

ax3 + by3 + cz3 = - 1

В матричной форме это выглядит так:

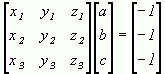
или

(3.2)

Решение этого уравнения дает значения коэффициентов уравнения плоскости:

Другой способ используется, если известен вектор нормали к плоскости, т. е.

n = ai + bj + ck

где i, j, k - единичные векторы осей x, y, z соответственно. Тогда уравнение плоскости примет вид

ax + by + cz + d = 0(3.3)

Величина d вычисляется с помощью произвольной точки на плоскости. В частности, если компоненты этой точки на плоскости (х1, y1, z1) то:

d = - (aх1 + by1 + cz1) (3.4)

Поскольку объем вычислений в алгоритмах удаления невидимых линий или поверхностей растет с увеличением числа многоугольников, для описания поверхностей выгодно использовать многоугольники с более чем тремя сторонами. Эти многоугольники могут быть как невыпуклыми, так и неплоскими. Метод, предложенный Мартином Ньюэлом, позволяет найти как точное решение для уравнений плоскостей, содержащих плоские многоугольники, так и “наилучшее” приближение для неплоских многоугольников. Этот метод эквивалентен определению нормали в каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов. Если a, b, c, d – коэффициенты уравнения плоскости, то

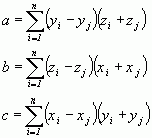(3.5)

где

if i =n then j = 1 else j = i + 1

а d вычисляется с помощью любой точки на плоскости.

Перед началом работы алгоритма удаления невидимых линий или поверхностей для получения желаемого вида сцены часто применяется трехмерное видовое преобразование. Матрицы тел для объектов преобразованной сцены можно получить или преобразованием исходных матриц тел или вычислением новых матриц тел, используя преобразованные вершины или точки.

Если [В] - матрица однородных координат, представляющая исходные вершины тела, а [Т] - матрица размером 4х4 видового преобразования, то преобразованные вершины таковы:

Рекомендуем скачать другие рефераты по теме: шпоры бесплатно, налоги и налогообложение.

Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата