Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата



x = Врем_х

проверим, что строка выше не является ни границей многоугольника, ни уже полностью заполненной; если это не так, то найти затравку, начиная с левого края подинтервала сканирующей строки

x = Xлев

y = y +1

while x £ Xправ

ищем затравку на строке выше

Флаг = 0

while ( Пиксел ( x, y ) ¹ Гран_значение and

Пиксел ( x, y ) ¹ Нов_значение and x < Xправ )

if Флаг = 0 then Флаг = 1

x = x + 1

end while

помещаем в стек крайний справа пиксел

if Флаг =1 then

if ( x = Xправ and Пиксел ( x, y ) ¹ Гран_значение and Пиксел ( x, y ) ¹ Нов_значение ) then

Push Пиксел ( x, y )

else

Push Пиксел ( x - 1, y )

end if

Флаг = 0

end if

продолжим проверку, если интервал был прерван

Xвход = x

while (( Пиксел ( x, y ) = Гран_значение or

Пиксел ( x, y ) = Нов_значение ) and x < Xправ)

x = x + 1

end while

удостоверимся что координата пиксела увеличена

if x = Xвход then x = x + 1

end while

проверим, что строка ниже не является ни границей многоугольника, ни уже полностью заполненной

Эта часть алгоритма совершенно аналогична проверке для строки выше, за исключением, того что вместо y = y + 1 надо подставить y = y -

end while

finish

Удаление невидимых линий и поверхностей

Задача удаления невидимых линий и поверхностей является одной из наиболее сложных в машинной графике. Алгоритмы удаления невидимых линий и поверхностей служат для определения линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства.

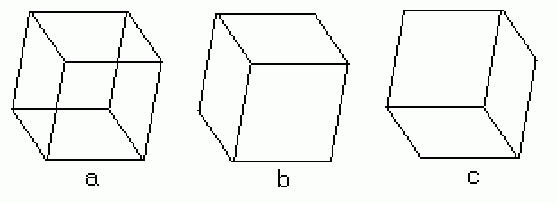
3.1 Необходимость удаления невидимых линий

Необходимость удаления невидимых линий, ребер, поверхностей или объемов проиллюстрирована рис.3.1. На рис.3.1, а приведен типичный каркасный чертеж куба. Его можно интерпретировать двояко: как вид куба сверху, слева или снизу, справа. Удаление тех линий или поверхностей, которые невидимы с соответствующей точки зрения, позволяют избавиться от неоднозначности. Результаты показаны на рис.3.1, b и c.

Сложность задачи удаления невидимых линий и поверхностей привела к появлению большого числа, различных способов ее решения. Многие из них ориентированы на специализированные приложения. Наилучшего решения общей задачи удаления невидимых линий и поверхностей не существует. Для моделирования процессов в реальном времени, например, для авиа тренажеров, требуются быстрые алгоритмы, которые могут порождать результаты с частотой видео генерации (30 кадр/с). Для машинной мультипликации требуются алгоритмы, которые могут генерировать сложные реалистические изображения, в которых представлены тени, прозрачность и фактура, учитывающие эффекты отражения и преломления цвета в мельчайших оттенках. Подобные алгоритмы работают медленно, и зачастую на вычисления требуется несколько минут или даже часов. Строго говоря, учет эффектов прозрачности, фактуры, отражения и т. п. не входит в задачу удаления невидимых линий или поверхностей. Естественнее считать их частью процесса визуализации изображения. Процесс визуализации является интерпретацией или представлением изображения или сцены в реалистической манере. Однако многие из этих эффектов встроены в алгоритмы удаления невидимых поверхностей и поэтому будут затронуты. Существует тесная взаимосвязь между скоростью работы алгоритма и детальностью его результата. Ни один из алгоритмов не может достигнуть хороших оценок для этих двух показателей одновременно. По мере создания все более быстрых алгоритмов можно строить все более детальные изображения. Реальные задачи, однако, всегда будут требовать учета еще большего количества деталей.

Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают. Алгоритмы, работающие в объектном пространстве, имеют дело с физической системой координат, в которой описаны эти объекты. При этом получаются весьма точные результаты, ограниченные, вообще говоря, лишь точностью вычислений. Полученные изображения можно свободно увеличивать во много раз. Алгоритмы, работающие в объектном пространстве, особенно полезны в тех приложениях, где необходима высокая точность. Алгоритмы же, работающие в пространстве изображения, имеют дело с системой координат того экрана, на котором объекты визуализируются. При этом точность вычислений ограничена разрешающей способностью экрана. Результаты, полученные в пространстве изображения, а затем увеличенные во много раз, не будут соответствовать исходной сцене. Алгоритмы, формирующие список приоритетов работают попеременно в обеих упомянутых системах координат.

Объем вычислений для любого алгоритма, работающего в объектном пространстве, и сравнивающего каждый объект сцены со всеми остальными объектами этой сцены, растет теоретически как квадрат числа объектов ( n2 ). Аналогично, объем вычислений любого алгоритма, работающего в пространстве изображения и сравнивающего каждый объект сцены с позициями всех пикселов в системе координат экрана, растет теоретически, как nN. Здесь n обозначает количество объектов (тел, плоскостей или ребер) в сцене, а N - число пикселов. Теоретически трудоемкость алгоритмов, работаюoих в объектном пространстве, меньше трудоемкости алгоритмов, работающих в пространстве изображения, при n < N. Поскольку N обычно равно ( 512 )2, то теоретически большинство алгоритмов следует реализовывать в объектном пространстве. Однако на практике это не так. Дело в том, что алгоритмы, работающие в пространстве изображения, более эффективны потому, что для них легче воспользоваться преимуществом когерентности при растровой реализации.

Далее дается изложение некоторых алгоритмов, работающих как в объектном пространстве, так и в пространстве изображения. Каждый из них иллюстрирует одну или несколько основополагающих идей теории алгоритмов удаления невидимых линий и поверхностей.

Алгоритм плавающего горизонта

Алгоритм плавающего горизонта чаще всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде

F ( x, у, z ) = 0

Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.

Существует много алгоритмов, использующих этот подход. Поскольку в приложениях в основном нас интересует описание поверхности, этот алгоритм обычно работает в пространстве изображения. Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат x, y или z.

Рекомендуем скачать другие рефераты по теме: шпоры бесплатно, налоги и налогообложение.

Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата