Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



mH = | ( xi + 1 )2 + ( yi )2 – R2 |

mH = | ( xi + 1 )2 + ( yi - 1 )2 – R2 |

mH = | ( xi )2 + ( yi - 1 )2 – R2 |

Вычисления можно упростить, если заметить, что в окрестности точки ( xi, yi ) возможны только пять типов пересечений окружности и сетки растра, приведенных на рис.2.6.

Разность между квадратами расстояний от центра окружности до диагонального пиксела ( xi + 1, yi - 1 ) и от центра до точки на окружности R2 равна

Как и в алгоритме Брезенхема для отрезка, для выбора соответствующего пиксела желательно использовать только знак ошибки, а не её величину.

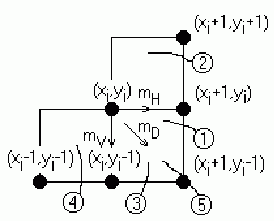
2.6 Пересечение окружности и сетки растра

При D < 0 диагональная точка ( xi + 1, yi - 1 ) находится внутри реальной окружности, т. е. это случаи 1 или 2 на рис.2.6. Ясно, что в этой ситуации следует выбрать либо пиксел ( xi + 1, yi ) т. е. mH, либо пиксел ( xi + 1, yi - 1 ), т. е. mD. Для этого сначала рассмотрим случай 1 и проверим разность квадратов расстояний от окружности до пикселов в горизонтальном и диагональном направлениях:

При d < 0 расстояние от окружности до диагонального пиксела

(mD) больше, чем до горизонтального (mH). Напротив, если d > 0, расстояние до горизонтального пиксела (mH) больше. Таким образом,

при d < 0 выбираем mH ( xi + 1, уi )

при d > 0 выбираем mD ( xi + 1, уi – 1 )

При d = 0, когда расстояния от окружности до обоих пикселов одинаковы, выбираем горизонтальный шаг.

Количество вычислений, необходимых для оценки величины d , можно сократить, если заметить, что в случае 1

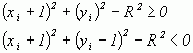
так как диагональный пиксел ( xi + 1, уi – 1 ) всегда лежит внутри окружности, а горизонтальный ( xi + 1, уi ) - вне ее. Таким образом, d можно вычислить по формуле

Дополнение до полного квадрата члена ( yi )2 с помощью добавления и вычитания - 2уi + 1 дает

В квадратных скобках стоит по определению D i, и его подстановка

d = 2(D i + yi) – 1

существенно упрощает выражение.

Рассмотрим случай 2 на рис.2.6 и заметим, что здесь должен быть выбран горизонтальный пиксел ( xi + 1, уi ), так как у является монотонно убывающей функцией. Проверка компонент d показывает, что

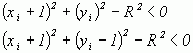
поскольку в случае 2 горизонтальный ( xi + 1, уi ) и диагональный ( xi + 1, уi – 1 ) пикселы лежат внутри окружности. Следовательно, d < 0, и при использовании того же самого критерия, что и в случае 1, выбирается пиксел ( xi + 1, уi ).

Если D i > 0, то диагональная точка ( xi + 1, уi – 1 ) находится вне окружности, т. е. это случаи З и 4 на рис.2.6. В данной ситуации ясно, что должен быть выбран либо пиксел ( xi + 1, уi – 1 ), т. е. mD, либо ( xi, уi – 1 ), т. е. mV. Аналогично разбору предыдущего случая критерий выбора можно получить, рассматривая сначала случай З и проверяя разность между квадратами расстояний от окружности до диагонального mD и вертикального mV пикселов, т. е.

При d < 0 расстояние от окружности до вертикального пиксела ( xi, уi – 1 ) больше и следует выбрать диагональный шаг mD, к пикселу ( xi + 1, уi – 1 ). Напротив, в случае d > 0 расстояние от окружности до диагонального пиксела больше и следует выбрать вертикальное движение к пикселу ( xi, уi – 1 ). Таким образом,

при d £ 0 выбираем mD в ( xi + 1, уi – 1 )

при d < 0 выбираем mV в ( xi, уi – 1 )

Здесь в случае d = 0, т. е. когда расстояния равны, выбран диагональный шаг.

Проверка компонент d показывает, что

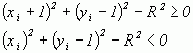
поскольку для случая З диагональный пиксел ( xi + 1, уi – 1 ) находится вне окружности, тогда как вертикальный пиксел ( xi, уi – 1 ) лежит внутри ее. Это позволяет записать d в виде

Дополнение до полного квадрата члена ( xi )2 с помощью добавления и вычитания 2xi + 1 дает

Использование определения D i приводит выражение к виду

Теперь, рассматривая случай 4, снова заметим, что следует выбрать вертикальный пиксел ( xi, уi – 1 ), так как y является монотонно убывающей функцией при возрастании x. проверка компонент d для случая 4 показывает, что

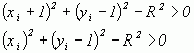
Рекомендуем скачать другие рефераты по теме: шпоры бесплатно, налоги и налогообложение.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата