Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



С помощью этого алгоритма получают прямые, вполне удовлетворительного вида, но у него есть ряд недостатков. Во-первых, плохая точность в концевых точках. Во-вторых, результаты работы алгоритма зависят от ориентации отрезка. Вдобавок предложенный алгоритм использует вещественную арифметику, что заметно снижает скорость выполнения.

Алгоритм Брезенхема

Алгоритм Брезенхема выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат - либо x, либо у (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние называется ошибкой.

Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис.2.1 это иллюстрируется для отрезка в первом

½ £ D y £ 1 (ошибка ³ 0)

0 £ D y/D x < ½ (ошибка D x then

Врем = D x

D x = D y

D y = Врем

Обмен = 1

else

Обмен = 0

end if

инициализация с поправкой на половину пиксела

= 2 * D y - D x

основной цикл

for i = 1 to D x

Plot ( x ,y )

While ( ³ 0 )

If Обмен = 1 then

x = x + s1

else

y = y + s2

end if

= - 2 * D x

end while

if Обмен = 1 then

y = y + s2

else

x = x + s1

end if

= + 2 * D y

next i

finish

Этот алгоритм удовлетворяет самым строгим требованиям. Он имеет приемлемую скорость и может быть легко реализован на аппаратном или микропрограммном уровне.

Алгоритм Брезенхема для генерации окружностей

В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т. е. окружностей, эллипсов, парабол, гипербол посвящено значительное число работ. Наибольшее внимание, разумеется, уделено окружности. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит

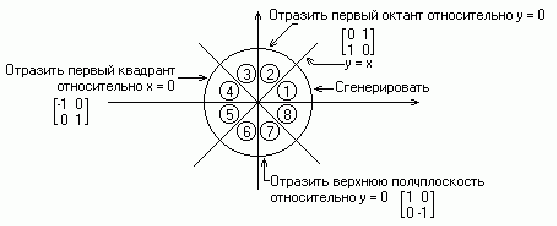
2.3 Генерация полной окружности из дуги в первом октанте

Брезенхему. Для начала заметим, что необходимо сгенерировать только одну восьмую часть окружности. Остальные её части могут быть получены последовательными отражениями, как это показано на рис. 2.3. Если сгенерирован первый октант (от 0° до 45° против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у = x, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой x = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = 0 для завершения построения. На рис.2.3. приведены двумерные матрицы соответствующих преобразований.

Для вывода алгоритма рассмотрим первую четверть окружности с центром в начале координат. Заметим, что если работа алгоритма начинается в точке x = 0, у = R, то при генерации окружности по часовой стрелке в первом квадранте у является монотонно убывающей функцией аргумента x (рис. 2.4). Аналогично, если исходной точкой является y = 0, x = R, то при генерации окружности против часовой стрелки x будет монотонно убывающей функцией аргумента у. В нашем случае выбирается генерация по часовой стрелке с началом в точке x = 0, у = R. Предполагается, что центр окружности и начальная точка находятся точно в точках растра.

Для любой заданной точки на окружности при генерации по часовой стрелке существует только три возможности выбрать следующий пиксел, наилучшим образом приближающий окружность: горизонтально вправо, по диагонали вниз и вправо, вертикально вниз. На рис.2.5 эти направления обозначены соответственно mH, mD, mV.

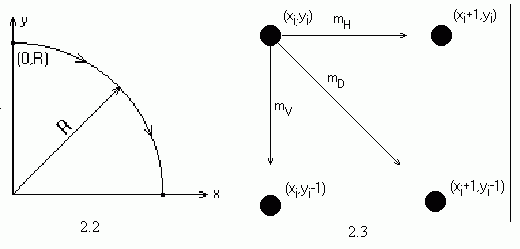
2.4 Окружность в первом квадранте. 2.5 Выбор пикселов в первом квадранте

Алгоритм выбирает пиксел, для которого минимален квадрат расстояния между одним из этих пикселов и окружностью, т. е. минимум из

Рекомендуем скачать другие рефераты по теме: шпоры бесплатно, налоги и налогообложение.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата