Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

где x0, y0 - центр круга, вокруг которого вводится пространственная окрестность, a, b - большая и фокальная полуоси описываемого эллипса соответственно, d - длина пространственной окрестности, x, y - координаты рассматриваемого примитива.

Как видно из сравнения формул (1.а, 1.б) и формул (2.а, 2.б), задание пространственных ограничений эллипсами аналогично предыдущему случаю, поэтому здесь справедливо все вышесказанное по отношению к ограничениям окружностями.

3) ограничения, задаваемые дугами окружностей:

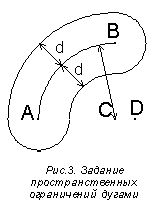
Этот случай аналогичен первому, только здесь вводятся еще два ограничения, связанных с углом к центру дуги окружности. Таким образом, примитивы множества E пространственной окрестности дуги должны удовлетворять условию:

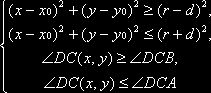,                      (3)

где C=(x0, y0) - центр дуги, вокруг которой вводится пространственная окрестность,

r - радиус дуги,

d -длина пространственной окрестности,

x, y - координаты рассматриваемого примитива,

A - точка, расположенная в начале дуги,

B - точка, расположенная в конце дуги,

D - точка, расположенная на одной оси с точкой ‘C’ со смещением

вправо, например (x0+1, y0).

Определение факта попадания примитива в пространственную окрестность, заданную дугами окружностей, при разрезании примитивов аналогично пространственным ограничениям из окружностей.

4) ограничения, задаваемые произвольными многоугольниками:

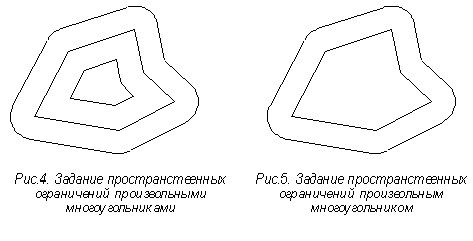
Как видно из рис.4-5 многоугольник, описывающий пространственную окрестность, не может быть получен простым масштабированием исходного контура (контура, описывающего заданный объект) по двум причинам:

a) для произвольного многоугольника, в общем случае, невозможно найти такую точку, которая была бы равноудалена от всех вершин этого многоугольника. Следовательно, нет такой точки, относительно которой операция масштабирования отодвинула бы стороны многоугольника, задающего пространственные ограничения, от сторон многоугольника-контура объекта на одинаковые расстояния.

b) стороны многоугольника, описывающего пространственную окрестность, как демонстрируют рис.4 и рис.5, ограничены дугами окружностей на внутренних углах, меньших .

Исходя из этих причин, предлагается следующий алгоритм, который учитывает все особенности преобразования контуров. Суть алгоритма заключается в следующем:

Из исходного множества вершин P (|P|=N) контура, описывающего заданный объект, строятся уравнения прямых (соответствующие формулы широко освещаются во всех печатных изданиях по машинной графике и аналитической геометрии, например, в [1-4]).

Согласно результатам, полученным в предыдущем пункте, строятся уравнения прямых многоугольника, задающего пространственные ограничения. Данные прямые смещены в направлении от контура объекта (см. случай, изображенный на рис. 5) и к контуру объекта (см. случай, изображенный на рис. 4). Уравнения прямых, параллельных ребрам многоугольного контура, можно построить по [4].

По формуле, аналогичной (1.б), определяются неравенства, ограничивающие отрезки полученного многоугольника в его углах.

Определяется множество V1 точек пересечения соседних отрезков и множество V2 точек пересечения отрезков и соответствующих окружностей, полученных из неравенств на шаге 3.

Рекомендуем скачать другие рефераты по теме: доклад, реферат на тему творчество.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата