Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Рассмотренные операции называются линейными.

Отметим некоторые свойства операций.

Пусть А,В,С – матрицы одинакового размера; a,b - действительные числа.

А+В = В+А – коммутативность сложения.

(А+В)+С = А+(В+С) – ассоциативность сложения.

Матрица О, состоящая из нулей, играет роль нуля: А+О=А.

Для любой матицы А существует противоположная –А, элементы которой отличаются от элементов А знаком, при этом А+( -А)=О.

a(bА) = (ab)А = (aА)b.          6. (a+b)А = aА+bА.

            7.   a(А+В) = aА+aВ.         8.  1* А = А.          9.   0 * А = 0.

Умножение матриц

В матричной алгебре важную роль играет операция умножения матриц, это весьма своеобразная операция.

Определение. Произведением матрицы А=(аij)  размера  и прямоугольной матрицы B=(bij)  размера   называется прямоугольная матрица С=(сij) размера , такая что cij=ai1+b1j+ ai2+b2j+…+ aik+bkj;  , .

Таким образом, элемент произведения матриц А и В, стоящий в i-ой строке и j-ом столбце, равен сумме произведений элементов i-ой строки первой матрицы А на соответствующие элементы j-ого столбца второй матрицы В т.е.

 .

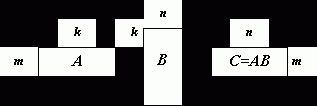Произведение С=АВ определено, если число столбцов матрицы А равно числу строк матрицы В. Это условие, а также размеры матриц можно представить схемой:

Очевидно, что операция умножения квадратных матриц всегда определена.

Примеры. Найдем произведения матриц АВ и ВА, если они существуют.

1.  , .

      

    

                                         

2.  , .

      

    

                                         

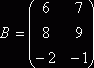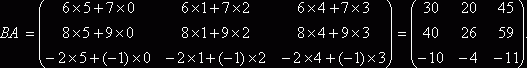
Рекомендуем скачать другие рефераты по теме: сочинение базаров, как оформить реферат.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата