Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

                ,  = 12-12 = 0;  А – вырожденная матрица.

Теорема. Произведение матриц есть вырожденная матрица тогда и только тогда, когда хотя бы один из множителей есть вырожденная матрица.

Необходимость. Пусть АВ – вырожденная матрица, т.е. =0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем  Это значит, что хотя бы одна из матриц А или В является вырожденной.

Достаточность. Пусть в произведении АВ матрица А вырожденная, т.е. =0. Найдем , т.к. =0; итак, =0; АВ - вырожденная матрица.

Замечание. Доказанная теорема справедлива для любого числа множителей.

Обратная матрица

Определение. Квадратная матрица В называется обратной по отношению к матрице А такого же размера, если

АВ = ВА = Е.          (1)

Пример. , .

               

В – матрица обратная к А.

Теорема. Если  для данной матрицы обратная существует, то она определяется однозначно.

Предположим, что для матрицы А существуют матрицы Х и У, такие, что

                                                     АХ = ХА = Е        (2)

АУ = УА = Е       (3)

Умножая одно из равенств, например, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Поскольку УА = Е, то ЕХ = УЕ, т.е.      Х = У. Теорема доказана.

Теорема (необходимое и достаточное условие существования обратной матрицы).

Обратная матрица А-1 существует тогда и только тогда, когда исходная матрица А невырожденная.

Необходимость. Пусть для матрицы А существует обратная А-1, т.е.                        А  А-1 = А-1А = Е. Тогда, ½А А-1½= ½А½½А-1½=½Е½=1, т.е. ½А½0 и ½А-1½0;       А – невырожденная.

Достаточность. Пусть дана невырожденная матрица порядка n

,

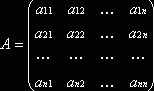так что ее определитель 0. Рассмотри матрицу, составленную из алгебраических дополнений к элементам матрицы А:

,

ее называют присоединенной к матрице А.

Следует обратить внимание на то, что алгебраические дополнения к элементам i-ой строки матрицы А стоят в i-ом столбце матрицы А*, для .

Найдем произведения матриц АА* и А*А. Обозначим АА* через С, тогда по определению произведения матриц имеем: Сij = аi1А 1j + а i2А 2j + … + а inАnj; i = 1, n: j = 1, n.

Рекомендуем скачать другие рефераты по теме: сочинение базаров, как оформить реферат.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата