Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

делим на коэффициент , в результате получаем уравнение

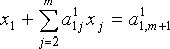
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент . В результате эти уравнения преобразуются к виду

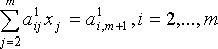
первое неизвестное оказалось исключенным из всех уравнений, кроме первого. Далее в предположении, что , делим второе уравнение на коэффициент  и исключаем неизвестное из всех уравнений, начиная со второго и т.д. В результате последовательного исключения неизвестных система уравнений преобразуется в систему уравнений с треугольной матрицей

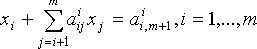
Совокупность проведенных вычислений называется прямым ходом метода Гаусса.

Из -го уравнения системы (2)  определяем , из ()-го уравнения определяем  и т.д. до . Совокупность таких вычислений называют обратным ходом метода Гаусса.

Реализация прямого метода Гаусса требует  арифметических операций, а обратного -  арифметических операций.

1.2 Итерационные методы решения СЛАУ

Метод итераций (метод последовательных приближений).

Приближенные методы решения систем линейных уравнений позволяют получать значения корней системы с заданной точностью в виде предела последовательности некоторых векторов. Процесс построения такой последовательности называется итерационным (повторяющимся).

Эффективность применения приближенных методов зависят от выбора начального вектора и быстроты сходимости процесса.

Рассмотрим метод итераций (метод  последовательных приближений). Пусть дана система n линейных уравнений с n неизвестными:

Ах=b,        (14)

Предполагая, что диагональные элементы aii  0 (i = 2, ..., n), выразим xi через первое уравнение систем x2 - через второе уравнение и т. д. В результате получим систему, эквивалентную системе (14):

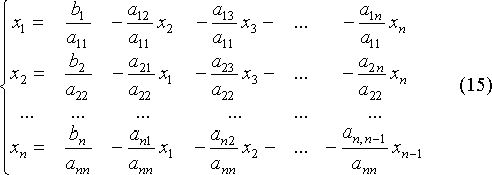
Обозначим ; , где i == 1, 2, ...,n; j == 1,2,..., n. Тогда система (15) запишется таким образом в матричной форме

Решим систему (16) методом последовательных приближений. За нулевое приближение примем столбец свободных членов. Любое (k+1)-е приближение вычисляют по формуле

Если последовательность приближений x(0),...,x(k) имеет предел , то этот предел является решением системы (15), поскольку в силу свойства предела , т.е.  [4,6].

Метод Зейделя.

Метод Зейделя представляет собой модификацию метода последовательных приближений. В методе Зейделя при вычислении (k+1)-го приближения неизвестного xi (i>1) учитываются уже найденные ранее (k+1)-е приближения неизвестных xi-1.

Пусть дана линейная система, приведенная к нормальному виду:

Рекомендуем скачать другие рефераты по теме: bestreferat ru, особенности реферата.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата