2. Алгоритм перебора L - классов
В
[?] и других работах развивается подход к анализу и решению задач
целочисленного программирования, основанный на регулярных разбиениях
пространства Rn. Много результатов было получено с помощью L-разбиения.
Дадим
определение L-разбиения. Пусть 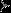 ,
, 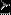 - символы
лексикографического порядка. Точки
- символы
лексикографического порядка. Точки 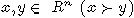 являются
L-эквивалентными, если не существует
являются
L-эквивалентными, если не существует 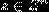 , такой что
, такой что 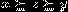 . Это
отношение разбивает любое множество
. Это
отношение разбивает любое множество 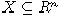 на классы
эквивалентности, которые называются L-классами. L-разбиение обладает рядом
важных свойств.
на классы
эквивалентности, которые называются L-классами. L-разбиение обладает рядом
важных свойств.
1)
Каждая точка 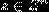 образует
отдельный L - класс. Остальные классы состоят только из нецелочисленных точек и
называются дробными.
образует
отдельный L - класс. Остальные классы состоят только из нецелочисленных точек и
называются дробными.
2)
Если X ограниченное множество, то фактор-множество X/L - конечно.
3)
L - разбиение согласовано с лексикографическим порядком, то есть для любого X
все элементы X/L могут быть линейно упорядочены следующим образом: 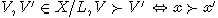 для всех
для всех 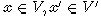 .
.
Если
X ограничено, то X/L можно представить в виде
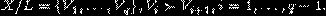
Рангом
L - класса V называется число 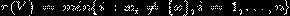 , если V
дробный L - класс и r(V) = n+1 для любой целой точки.
, если V
дробный L - класс и r(V) = n+1 для любой целой точки.
Алгоритм
перебора L - классов основан на идее поиска элемента L - разбиения, непосредственно следующего за данным L - классом в порядке лексикографического
возрастания (для задачи на минимум).
Пусть
 . Рассмотрим
этот метод более подробно для многогранника
. Рассмотрим
этот метод более подробно для многогранника 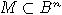 . Задача
булева программирования (БП) имеет вид:
. Задача
булева программирования (БП) имеет вид:
|
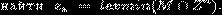
|
|
|
(5)
|
Соответствующая
задача линейного программирования (ЛП) состоит в нахождении лексикографически
минимального элемента множества M.
Пусть
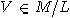 и известен
некоторый представитель
и известен
некоторый представитель 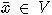 . Сначала мы
ищем соседний к V дробный элемент V' такой, что
. Сначала мы
ищем соседний к V дробный элемент V' такой, что 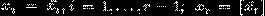 где r - ранг
класса V, и x - некоторая точка из V'. Если V' будет найден, продолжаем процесс
для V' вместо V.
где r - ранг
класса V, и x - некоторая точка из V'. Если V' будет найден, продолжаем процесс
для V' вместо V.
В
противном случае мы ищем V' такой, что  , - ранг V',
, - ранг V',  . Если V' не
может быть найден, мы уменьшаем (если это возможно) r' на 1 и продолжаем просмотр.
Если V' будет найден, мы возвращаемся к началу процедуры и V' становится
исходным L - классом.
. Если V' не
может быть найден, мы уменьшаем (если это возможно) r' на 1 и продолжаем просмотр.
Если V' будет найден, мы возвращаемся к началу процедуры и V' становится
исходным L - классом.
Если
не существует соседнего дробного L-класса, то либо мы получаем оптимум задачи
БП, либо приходим к выводу, что задача не имеет решения. Процесс является
конечным, так как M ограничено.
Опишем
алгоритм перебора L - классов. Для простоты номер итерации будем опускать.
Шаг
0. Решаем исходную задачу ЛП. Если она не имеет решения или ее решение
целочисленное, процесс завершается. В противном случае идем на шаг 1.
Шаг
1. Обозначим через 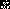 оптимальное
решение задачи ЛП, которая рассматривалась на предыдущем шаге. Находим
оптимальное
решение задачи ЛП, которая рассматривалась на предыдущем шаге. Находим

 Главная
Главная