Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Величину rn(x) называет остаточным членом. Видно, что при тех же значениях х, для которых rn(x) достаточно мал, вместо f(x) можно рассматривать многочлен Pn(x).

Оценим величину остаточного члена rn(x). Запишем его в виде

,

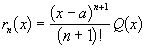где Q(x)- функция, которую нужно определить. Формула примет вид:

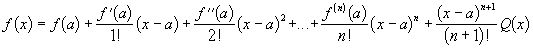
При фиксированных значениях а и х функция Q(x) имеет определённые значения, которые обозначаются через Q.

Рассмотрим вспомогательную функцию переменной t (a<t<x)

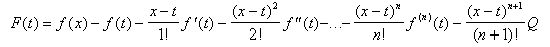
Применяя правила дифференцирования алгебраической суммы и произведения двух функций, находим производную функции F(t) по аргументу t.(x и а- фиксированные, следовательно, f(x)- постоянная).

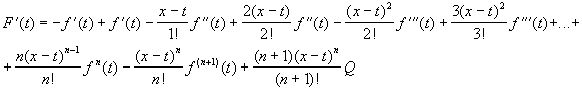
Приведя подобные слагаемые, получим:

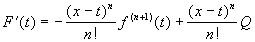
Из формулы функции F(t) видно, что F(x)=0 и F(a)=0. Воспользуемся свойством дифференцируемой функции:

Если дифференцируемая функция f(x) обращается в нуль при х=а и х=b, f(a)=0, f(b)=0, (a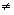b), то между точками а и b найдётся по крайней мере одна т.с, в которой равна нулю производная данной функции: f'(c )=0. (т. Ролля).

Геометрически это означает, если в т. а и b f(a)=0 и f(b)=0, то 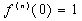такое, что в т. С(с,f(c )) касательная к графику y=f(x) параллельна оси ОХ.

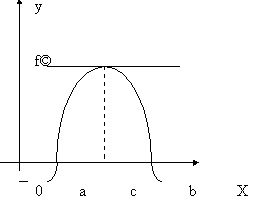
Корнем или нулём функции называют такое значение аргумента х0 , при котором функция f(x0)=0.

С учётом этого понятия указанное свойство можно сформулировать так: между двумя различными корнями дифференцируемой функции находится хотя бы один корень её производной (т. Ролля).

Поскольку F(x)=0 и F(a)=0, то к функции F(t) можно применить свойство: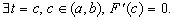

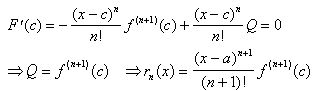
Так как с заключено между а и х, то его можно представить в виде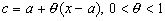

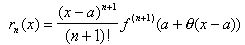
Говорят, что это равенство выражает остаточный член формулы в форме Лагранжа. Подставим его в формулу:

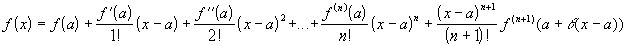
Эту формулу называют формулой Тейлора с остаточным членом в форме Лагранжа.

Если а=0, то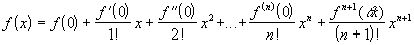

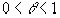
Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата