Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

если f(x) непрерывна в конечном замкнутом интервале [a,b], то всякому 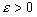можно сопоставить полином Pn(x) степени n=n(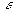), для которого во всём интервале [a,b] имеет место неравенство .

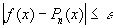Не нарушая общности, примем, что а=0, b=1. Приведём доказательство С.П.Бернштейна.

Для этого построим полином 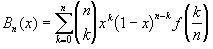, 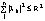и докажем, что равномерно во всём интервале [0,1] 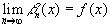. Напишем тождества:

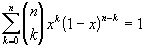(1); 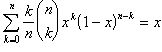;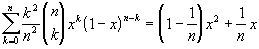, из которых последите два получаются дифференцированием по р соотношения:

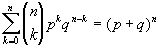. Из написанных тождеств вытекает, что 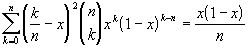(2).

Умножая (1) на f(x) и отнимая Bn(x), получим, что

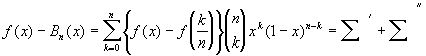, где суммирование в распространено на те значения к, для которых 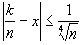, а суммирование в 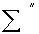- на остальные значения к.

Так как f(x) непрерывна в замкнутом интервале [0,1], и, значит, ограничена: 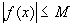во всём этом интервале, то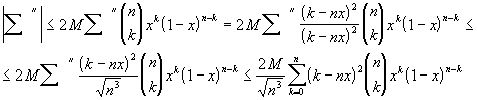

А это выражение на основании (2): 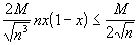, с другой стороны,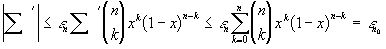, где 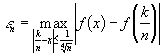, и, значит, 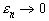при .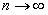

Окончательно: 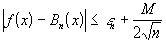, что и доказывает теорему Вейерштрасса.

Заметим, что если Pn(x) равномерно стремится к f(x) при 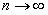, то f(x) разлагается в равномерно сходящийся ряд.

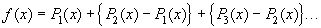
Поэтому т. Вейерштрасса состоит так же в том, что всякая непрерывная в конечном интервале [a,b] функция f(x) может быть разложена в равномерно сходящийся при 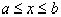ряд, члены которого- полиномы.

1.4. Вторая теорема Вейерштрасса.

Она относится к периодическим непрерывным функциям:

Если F(t)- непрерывная функция с периодом 2, то каково бы ни было число 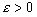, существует тригонометрическая сумма 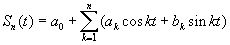, n=n(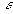), которая для всех t удовлетворяет неравенству:

.

II. Круг идей П.Л. Чебышева.

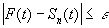Пусть даны замкнутый (конечный или бесконечный) интервал [a,b] числовой оси и две вещественные непрерывные в [a,b] функции f(x) и S(x). Составим выражение: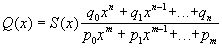 (*), где m и n заданы и поставим задачу найти вещественные параметры p0,p1...pm; q0,q1...qn так, чтобы уклонение 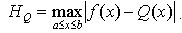Q(x) от f(x) было наименьшим.

В частном случае, когда S(x)=1, m=0 и интервал [a,b] конечен, поставленная задача переходит в задачу о наилучшем приближении в пространстве С заданной функции с помощью многочлена степени n.

Будем полагать, что m=n-k, кроме того, если интервалом [a,b] является вся числовая ось, мы будем предполагать, что 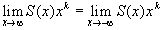и будем рассматривать только те функции, для которых 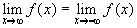, m условимся считать чётным.

2.1 Обобщённая теорема Валле-Пуссена.

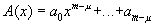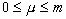Если многочлены ; , где и 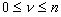, , 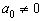не имеют общего делителя , а выражение 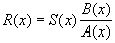в интервале [a,b] остаётся конечным и если разность f(x)-R(x) принимает в последовательных точках x1<x2<...<xn интервала [a,b], отличные от значения 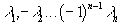с чередующимися знаками, N=m+n-d+2, 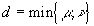, то для каждой функции 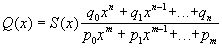имеет место неравенство: 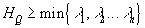, где 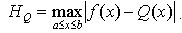. Это же неравенство имеет место, если R(x)=0 и N=n+2.

Значение этой теоремы состоит в том, что она даёт возможность получить для погрешности наилучшего приближения некоторую оценку снизу.

Теорема существования.

Среди функций Q(x) существует по крайней мере одна, для которой HQ имеет наименьшее значение.

Т.о., пусть Н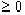- есть нижняя грань множества всех HQ. По определению, следовательно, существует бесконечная последовательность функций Qi(x), для которой .

2.2. Теорема Чебышева.

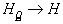Функция Р(х), которая из всех функций вида Q(x) наименее уклоняется в [a,b] от функции f(x), единственна.

Эта функция вполне характеризуется таким своим свойством, если она приведена к виду 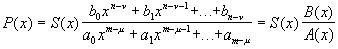, 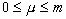и 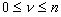, 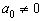и дробь 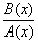несократима, то число N последовательных точек интервала [a,b], в котором разность f(x)-P(x) принимает с чередующимися знаками значение Нр, не менее, чем m+n-d+2, где d=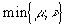, а если P(x)=0, то .

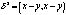Рекомендуем скачать другие рефераты по теме: поняття реферат, дипломная работа школа.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата