Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Формулы сложения дают выражения для суммы или разности двух  (или нескольких) аркфункций через какую-либо данную аркфункцию. Пусть дана сумма аркфункций; над этой суммой можно выполнить любую тригонометрическую операцию. (....) В соответствии с этим дуга-функция может быть выражена посредством любой данной аркфункции. Однако в различных случаях (при одних и тех же аркфункциях) могут получаться различные формулы, в зависимости от промежутка, в котором берется значение рассматриваемой аркфункции.

Сказанное пояснено ниже на числовых примерах.

Примеры.

Пример №1. Преобразовать в арксинус сумму

Решение: эта сумма является суммой двух дуг α и β, где

; 

В данном случае  (т.к. , а следовательно, ), а также , поэтому .

Вычислив синус дуги γ, получим:

Т.к. сумма γ заключена на сегменте [-π/2; π/2], то

Пример №2. Представить дугу γ, рассмотренную в предыдущем примере, в виде арктангенса. Имеем:

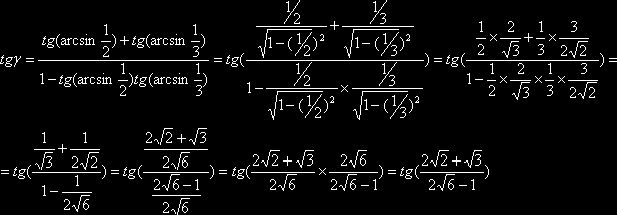
Откуда

Пример №3. Представить посредством арктангенса сумму

Решение: в данном случае (в отличие от предыдущего) дуга γ оканчивается во второй четверти, т.к. , а . Вычисляем

В рассматриваемом примере , так как дуги γ и заключены в различных интервалах,

, а

В данном случае

Пример №4. Представить дугу γ, рассмотренную в предыдущем примере, в виде арккосинуса.

Решение: имеем

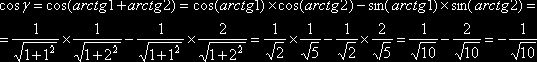
Обе дуги γ и расположены в верхней полуокружности и имеют одинаковый косинус, следовательно, эти дуги равны:

Рекомендуем скачать другие рефераты по теме: диплом рф, реферат на тему жизнь.





Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата