Билеты по геометрии БИЛЕТ 1

А1 Какова бы ни была плоскость, существуют точки принадлежащие этой плоскости и точки, не принадлежащие ей.

А2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

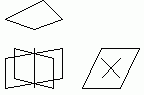
А3 Если две различные прямые имеют общую точку, то ч/з них можно провести плоскость, и притом только одну.

БИЛЕТ 2

ОПРЕДЕЛЕНИЕ. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

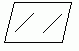
ТЕОРЕМА. Через точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Док-во: проведем ч/з а и М плоскость a , а ч/з М в плоскости a прямую b| a. Докажем, что b| a единственна.

Допустим, что существует другая прямая b2| a, и проходящая ч/з т.М. Через b2 и а можно провести плоскость a 2, которая проходит ч/з М и а, след-но, по Т.14.1(ЧЕРЕЗ ПРЯМ. И ТОЧКУ НЕ ЛЕЖ. НА ЭТОЙ ПРЯМОЙ МОЖНО ПРОВЕСТИ ПЛОСКОСТЬ И ПРИТОМ ТОЛЬКО ОДНУ) она совпадает с a . По аксиоме о параллельных прямых b2 и а совпадают. Ч.Т.Д.

БИЛЕТ 3

ОПРЕДЕЛЕНИЕ. Прямая и плоскость называются параллельными, если они не имеют общих точек.

ТЕОРЕМА. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Док-во: Пусть a -плоскость, а - не лежащая в ней прямая и а1 - прямая в плоскости a ,параллельная прямой а.

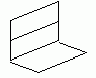
Проведем плоскость a 1 ч/з прямые а и а1.

Она отлична от a , т.к. прямая а не лежит в плоскости a . Плоскости a и a 1 пересекаются по прямой а1. Если бы прямая а пересекала плоскость a , то точка пересечения принадлежала бы прямой а1. Но это невозможно, т.к. прямые а и а1 параллельны. Итак, прямая а не пересекает плоскость a , а значит, параллельна плоскости a . Ч.Т.Д.

БИЛЕТ 4

ОПРЕДЕЛЕНИЕ. Две плоскости называются параллельными, если они не пересекаются.

ТЕОРЕМА. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

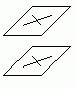
Док-во: Рассмотрим две плоскости a и b . В плоскости a лежат пересекающиеся в т.М прямые a и b, а в b - прямые а1 и b1, причем а| а1 и b| b1.

Докажем, что плоскоскоти a и b не параллельны. Тогда они перес. по прямой с. Мы получили, что плоскость a проходит ч/з прямую а, параллельную плоскости b , и пересекает плоскость b по прямой с. Отсюда следует, что а| с.

Но плоскость a проходит также ч/з прямую b, параллельную плоскости b . Поэтому b | с. Таким обр. ч/з т.М проходят две прямые а и b, | с. Но это невозможно, т.к. по теореме о параллельных прямых ч/з т. М проходит только

БИЛЕТ 5

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

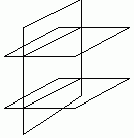
Для док-ва данного св-ва рассмотрим прямые а и b , по которым параллельные плоскости a и b пересекаются с плоскостью j . Докажем, что а| b.

Эти прямые лежат в одной плоскости (j ) и не пересекаются. В самом деле, если бы прямые а и b пересекались, то пл. a и b имели бы общ. точку, что невозможно, т.к. a | . Итак, прямые а и b лежат в одной плоскости и не пересекаются, а| b.

2. Vпирамиды= 1/3*Sосн.*H

БИЛЕТ 6

Отрезки параллельных прямых, заключенные м/у параллельными плоскостями, равны.

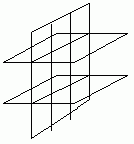
Для док-ва рассмотрим отрезки АВ и СD двух параллельных прямых, заключенные м/у параллельными плоскостями a и b . Докажем, АВ=СD. Плоскость j , проходящая ч/з параллельные прямые АВ и СD, пересекается с плоскостями a и b по параллельным прямым АС и ВD. Таким образом, в четырехугольнике ABDC противолеж. стор. паралл., т.е. ABDC-параллел-м

Но в пар-ме прот. леж. стороны равны, значит AB=CD.

Sп.п.=2p R(H+R)

Рекомендуем скачать другие рефераты по теме: доклад по обж, изложение по русскому 7 класс.





1  2  3  4 | Следующая страница реферата