Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата



БИЛЕТ 7

Сформулируем основные св-ва параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой L.

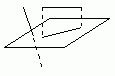
10 Проекция прямой есть прямая.

20 Проекция отрезка есть отрезок.

30 Проекции параллельных отрезков - параллельные отрезки или отрезки, принадлеж. одной прямой.

40 Проекции параллельных отрезков, а также проекции отрезков, лежащих на одной прямой, пропорциональны самим отрезкам.

Из св-ва 40 следует, что проекция середины отрезка есть середина проекции отрезка.

БИЛЕТ 8

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

ТЕОРЕМА: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

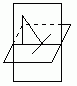
БИЛЕТ 9

ТЕОРЕМА: Прямая, проведенная в плоскости ч/з основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной

Док-во: AH - перпенд. к плоскости a , AM - наклонная, а – прямая проведенная в плоск. a ч/з точку M перпенд к проекцииHM наклонной.

Рассмотрим плоск. AMH. Прямая а^ этой плоскости, т.к. она ^ к двум пересекающимся прямым AH и MH. Отсюда след. что прямая а перпендикулярна к любой прямой, лежащей в плоскости AMH, в частности а^ AM. Ч.Т.Д.

БИЛЕТ 10

ТЕОРЕМА: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

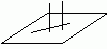
Док-во: Рассмотрим две параллельные прямые а и а1 и плоскость a , такую, что а^ a . Докажем, что и а1^ a .

Проведем какую-нибудь прямую х в плоскости a .

Так как а^ a , то а^ х. Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости a , т.е. а1^ a . Ч.Т.Д.

Vпаралл-да=abc=Sосн.*H

БИЛЕТ 12

ОПРЕДЕЛЕНИЕ: Две пересекающиеся плоскости называются перпендикулярными, если угол м/у ними равен 900.

ТЕОРЕМА: Если одна из двух плоскостей проходит ч/з прямую,перпендикулярную плоскости, то такие плоскости перпендикулярны.

Док-во: Рассмотрим плоскости a и b такие, что плоскость a проходит ч/з прямую АВ, перпендикулярную к плоскости b и пересекающуюся с ней в точке А. Докажем, что a ^ b . Плоскости a и b пересекаются по прямой АС, причем АВ^ АС, Т.к. по усл. АВ^ b , и, значит, прямая АВ^ к любой прямой, лежащей в плоскости b .

Проведем в плоскости b прямую АD,^ АС. Тогда Р BAD - линейный угол двугранного угла, образованного при пересечении плоскостей a и b . Но Р BAD=900 (т.к. AB^ b ). След-но, угол м/у плоскостями a и b равен 900, т.е. a ^ b . Ч.Т.Д.

Sбок=P*a (а - бок. ребро, Р-периметр)

БИЛЕТ 11

ТЕОРЕМА: Если две прямые перпендикулярны плоскости, то они параллельны.

Док-во: Рассмотрим прямые а и b, перпендикулярные к плоскости a . Докажем, что аЅ Ѕ b.

Через какую-нибудь точку М прямой b проведем прямую b 1, параллельную прямой a . Докажем, что прямая b 1 совпадает с прямой b . Тем самым будет доказано, что a Ѕ Ѕ . Допустим, что прямые b и b 1 не совпадают. Тогда в плоскости b , содержащей прямые b и b 1, ч/з точку М проходят две прямые, перпендикулярные к прямой c , по которой пересекаются плоскости a и b . Но это невозможно, след-но, a Ѕ Ѕ . Ч.Т.Д.

БИЛЕТ 13

ОПРЕДЕЛЕНИЕ: Расстояние м/у одной из скрещивающихся прямых и плоскостью, проходящей ч/з другую прямую параллельно первой, называется расстоянием м/у скрещивающимися прямыми.

Рекомендуем скачать другие рефераты по теме: доклад по обж, изложение по русскому 7 класс.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата