Быстродействующий адаптивный наблюдатель в системе компенсации неизвестного запаздывания

А.В. Старосельский, Московский Государственный Институт Электроники и Математики

Настоящая работа посвящена построению системы компенсации неизвестного запаздывания. Наличие большого запаздывания, как известно [1], отрицательно сказывается на работоспособности системы управления.

Для компенсации неизвестного запаздывания разработана адаптивная система, состоящая из быстродействующего адаптивного наблюдателя, вычисляющего оценки неизвестных параметров и запаздывания системы управления, и прогнозатора Смита, компенсирующего это запаздывание.

Центральным моментом работы является построение алгоритма быстродействующего адаптивного наблюдателя для оценивания неизвестного запаздывания, так как прогнозатор Смита применим лишь в тех случаях, когда запаздывание априори известно. Этот алгоритм основан на использовании метода настраиваемой модели. Суть алгоритма изложена ниже.

Пусть поведение интересующего нас объекта описывается следующим дифференциальным уравнением:

, (1)

;

Здесь a1=3, a0=2 - известные постоянные коэффициенты;  - неизвестные постоянные. Тогда структурная схема соответствующего процесса управления будет иметь вид, представленный на рис. 1. Здесь приборному измерению доступны вход xd(t) и выход x(t) системы управления.

Построим быстродействующий адаптивный наблюдатель для идентификации неизвестных параметров системы , а также прогнозатор Смита для компенсации запаздывания , после чего будем подставлять получаемые наблюдателем оценки  в прогнозатор.

   

– 

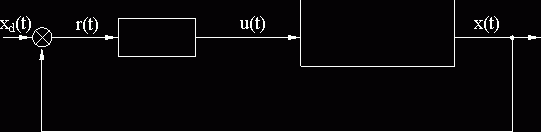
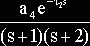
Рис 1. Система управления для объекта с неизвестным запаздыванием.

 

y(t)

v(t) –

 +

–

  

–

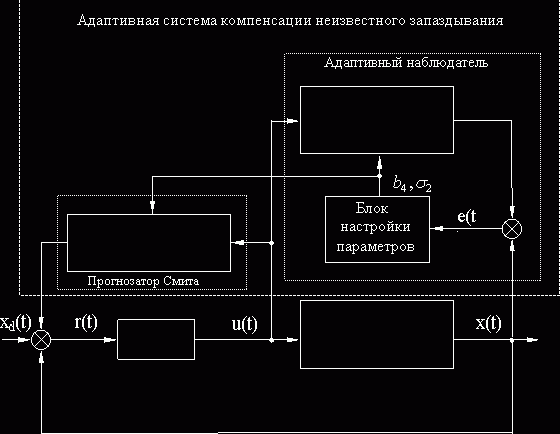
Рис. 2. Адаптивная система компенсации неизвестного запаздывания.

На каждом из подынтервалов времени функционирования системы Jj настраиваемую модель опишем следующими уравнениями:

  (2)

,

где  - параметры модели, настраиваемые соответственно на параметры  объекта (1).

Рекомендуем скачать другие рефераты по теме: курсовые работы бесплатно, решебник по геометрии.





1  2  3 | Следующая страница реферата