Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Если начальная скорость равна нулю (), то отклонение  есть сумма левой и правой бегущих волн, причем начальная форма обеих волн определяется функцией , равной половине начального отклонения. Если же , то  представляет возмущение струны, создаваемое начальной скоростью.

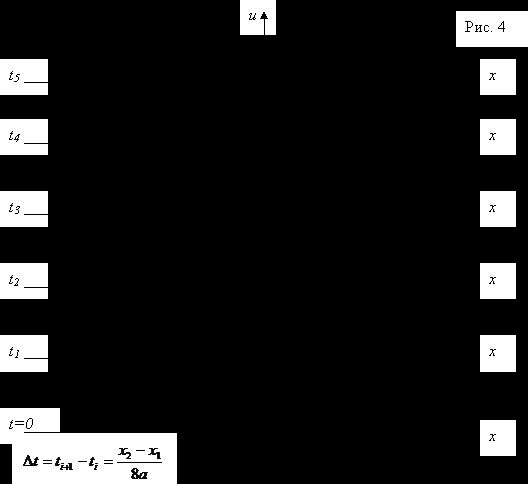
Рассмотрим распространение начального отклонения, заданного в виде равнобедренного треугольника. Такой начальный профиль можно получить, если оттянуть струну в середине отрезка  . На рис. 4 даны последовательные положения струны через промежутки времени .

Наглядное представление о характере процесса распространения можно получить с помощью фазовой плоскости (x, t). Проведем характеристики через точки  и ; они разобьют полуплоскость  на шесть областей (рис. 5).

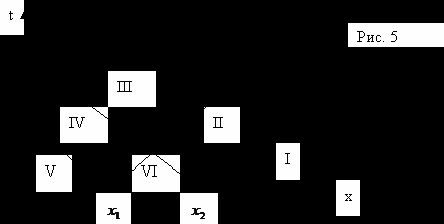
Отклонение  в любой точке (x,t) дается формулой (12). Поэтому в областях I, III, V отклонение равно нулю, так как характеристический треугольник любой точки из этих областей не имеет общих точек с отрезком , на котором заданы начальные условия. В области II решением является «правая волна» , в области IV – «левая волна» , а в области VI решение есть сумма «левой» и «правой» волн.

3. О колебании стержней.

В курсах методов математической физики основное место отводится уравнениям второго порядка. Однако большое число задач о колебаниях стержней, пластин и т.д. приводит к уравнениям более высокого порядка.

В качестве примера на уравнения 4-го порядка рассмотрим задачу о собственных колебаниях камертона, эквивалентную задаче о колебаниях тонкого прямоугольного стержня, зажатого одним концом в массивные тиски. Определение формы колебаний камертона и его частоты сводится к решению «уравнения поперечных колебаний стержня»

 (1)

К этому уравнению приходят во многих задачах о колебании стержней, при расчете устойчивости вращающихся валов, а также при изучении вибрации кораблей.

Приведем элементарный вывод уравнения (1). Рассмотрим прямоуголный стержень длиной , высотой h и шириной b. Выделим элемент длины dx. После изгиба торцевые сечения выделенного элемента стержня, предполагаемые плоскими, образуют угол , Если деформации малы, а длина оси стержня при изгибе не меняется (dl=dx), то

.

Слой материала, отстоящий от оси стержня y=0 на расстоянии , изменяет свою длину на величину . По закону Гука сила натяжения, действующая вдоль слоя, равна

,

где E – модуль упругости материала стержня. Полный изгибающий момент сил, действующих на сечение x, равен

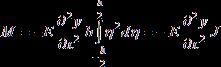, (2)

где

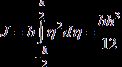
- момент инерции прямоугольного сечения относительно своей горизонтальной оси. Обозначим через M(x) момент, действующих на правую часть стержня в каждом сечении. В сечении x+dx, очевидно, действует момент сил, равный –(M+dM).

Избыточный момент –dM уравновешивается моментом тангенциальных сил

.

Отсюда в силу равенства (2) получаем величину тангенциальной силы

. (3)

Приравняв действующую на элемент результирующую силу

Рекомендуем скачать другие рефераты по теме: фонды реферат, соціологія шпори.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата