Предыдущая страница реферата | 1  2  3  4  5  6

Эта однородная система имеет нетривиальные решения A и B, если определитель системы равен нулю. Приравнивая этот определитель нулю, получаем трансцендентное уравнение для вычисления собственных значений

.

Так как , то это уравнение можно записать в идее

 (). (10)

Корни уравнения (10) без труда вычисляются, например, графически

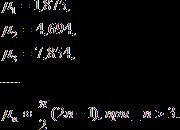
Последняя формула дает значение  с точностью до трех десятичных знаков, начиная с n=3, и с точностью до шестого знака для .

Рассмотрим теперь частоты колебаний камертона. Уравнению

Удовлетворяют тригонометрические функции

с частотой

,

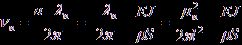Частоты  собственных колебаний относятся как квадраты . Так как

,

То второй собственный тон выше основного тона более чем на две с половиной октавы, т.е. выше шестой гармоники струны при равном основном тоне, третье же собственное колебание выше основного тона более чем на четыре октавы. Например, если камертон имеет основную частоту в 440 колебаний в секунду (принятый стандарт a’ – ноты ля первой октавы), то следующая собственная частота камертона будет 2757,5 колебания в секунду (между c’’’’ =2637,3 и f’’’’=2794,0 – между нотами ми и фа четвертой октавы равномерно-темперированной гаммы), третья же собственная частота в 7721,1 колебания в секунду уже выходит за пределы шкалы собственно музыкальных звуков.

При возбуждении колебаний камертона ударом присутствует не только первая, но и высшие гармоники, чем и объясняется металлический звук в начальный момент. Однако с течением времени высшие гармоники быстро затухают и камертон издает чистый звук основного тона.

4. Заключение.

Дифференциальные уравнения с частными производными широко применяются в математической физике. В качестве примера в данной работе рассмотрены два уравнения.

Волновое уравнение с краевыми условиями можно свести к решению формулы Даламбера, задающуюся начальными условиями. И с помощью фазовой плоскости можно отследить характер его решения.

В процессе решения «уравнения поперечных колебаний стержня» получаем задачу о собственных значениях и задачу о нахождение частот собственных колебаний. Причем частоты собственных колебаний относятся как квадраты собственных значений.

Список литературы

А. Н. Тихонов, А. А. Самарский «Уравнения математической физики», Москва, 1966 г.

Н. С. Пискунов «Дифференциальное и интегральное исчисление», Москва, 1970 г.

Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов «Уравнения в честных производных математической физики», Москва, 1970 г.

Скачали данный реферат: Салтанов, Evgenij, Адолия, Павленко, Салагин, Котенко.
Последние просмотренные рефераты на тему: дипломная работа, жизнь человека реферат, контроль реферат, доклад по биологии.





Предыдущая страница реферата | 1  2  3  4  5  6