
Дзета-функция Римана
| Категория реферата: Рефераты по математике
| Теги реферата: bestreferat, сочинения по русскому языку
| Добавил(а) на сайт: Петронилла.
Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата
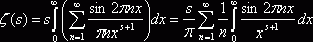 . Сделаем в полученном интеграле подстановку
. Сделаем в полученном интеграле подстановку ![]() , отсюда следует
, отсюда следует ![]() , а
, а ![]() , и получим далее
, и получим далее 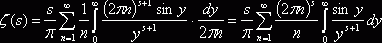 . Известно, что
. Известно, что 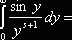
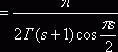 , значит
, значит 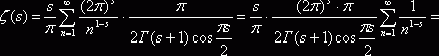
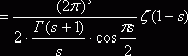 . Из известного соотношения для гамма-функции
. Из известного соотношения для гамма-функции ![]() , по формуле дополнения
, по формуле дополнения ![]() , следовательно
, следовательно ![]()
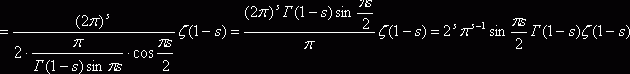
Итак, мы получили функциональное уравнение дзета-функции Римана
![]() (7),
(7),
которое само по себе может служить средством изучения этой
функции, так как вполне характеризует её, в том смысле, что любая другая
функция ![]() , удовлетворяющая равенству (7), а также ещё некоторым естественным
условиям, тождественна с
, удовлетворяющая равенству (7), а также ещё некоторым естественным
условиям, тождественна с ![]() .
.
Пока, правда, как следует из рассуждений, мы доказали
формулу (7) для ![]() . Однако правая часть этого равенства является аналитической
функцией s и при
. Однако правая часть этого равенства является аналитической
функцией s и при ![]() . Это показывает, что дзета-функция может быть аналитически
продолжена на всю комплексную плоскость, причём не имеет на ней никаких особенностей, кроме упоминавшегося полюса при
. Это показывает, что дзета-функция может быть аналитически
продолжена на всю комплексную плоскость, причём не имеет на ней никаких особенностей, кроме упоминавшегося полюса при ![]() .
.
Чтобы доказательство было строгим, мы должны ещё обосновать
почленное интегрирование. Поскольку ряд (6) сходится почти всюду и его
частичные суммы остаются ограниченными, почленное интегрирование на любом конечном
отрезке допустимо. Ввиду 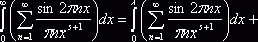
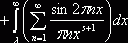 для любого
для любого ![]() , остаётся доказать, что
, остаётся доказать, что 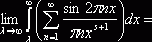
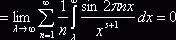 при
при ![]() . Но интегрируя внутренний интеграл по частям имеем
. Но интегрируя внутренний интеграл по частям имеем 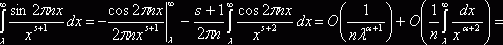
![]() . Отсюда без труда получается наше утверждение.
. Отсюда без труда получается наше утверждение.
Функциональное уравнение дзета-функции (7) может быть записано многими способами. Например, заменим s на 1-s, получаем равносильное равенство
![]() (8). Из него можно получить два небольших следствия.
(8). Из него можно получить два небольших следствия.
Подставим в (8) вместо s
число 2m, где m – натуральное
число. Имеем ![]() . По формуле (4) первой главы
. По формуле (4) первой главы ![]()
![]() , а
, а ![]() , поэтому
, поэтому ![]() и произведя в правой
части все сокращения, учитывая, что
и произведя в правой
части все сокращения, учитывая, что ![]() , получим
, получим ![]() .
.
Покажем ещё, что ![]() . Для этого прологарифмируем равенство (8):
. Для этого прологарифмируем равенство (8): ![]()
![]() и результат
продифференцируем
и результат
продифференцируем ![]()
![]() . В окрестности точки s=1
. В окрестности точки s=1
![]() ,
, ![]()
![]() ,
, 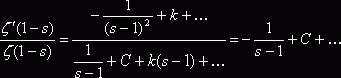 , где С – постоянная Эйлера, а k
– произвольная постоянная. Следовательно, устремляя s
к единице, получим
, где С – постоянная Эйлера, а k
– произвольная постоянная. Следовательно, устремляя s
к единице, получим ![]() , то есть
, то есть ![]() . Опять из формулы (4) главы 1 при k=0
. Опять из формулы (4) главы 1 при k=0
![]() , значит, действительно,
, значит, действительно, ![]() .
.
Глава 3.
Как уже было сказано, дзета-функция Римана широко применяется в математическом анализе. Однако наиболее полно важность её выявляется в теории чисел, где она оказывает неоценимую помощь в изучении распределения простых чисел в натуральном ряду. К сожалению, рассказ о серьезных и нетривиальных применениях дзета-функции Римана выходит за рамки этой работы. Но чтобы хотя бы немного представить мощь этой функции, докажем с её помощью несколько интересных утверждений.
Например, известно, что простых чисел бесконечно много. Самое знаменитое элементарное доказательство принадлежит Евклиду. Оно состоит в следующем. Предположим, что существует конечное число простых чисел, обозначим их p1, p2, … , pn. Рассмотрим число p1p2…pn+1, оно не делится ни на одно из простых и не совпадает ни с одним из них, то есть является простым числом, отличным от вышеуказанных, что противоречит предположению. Значит, количество простых чисел не может быть конечным.
Другое доказательство этого факта, использующее
дзета-функцию, было дано Эйлером. Рассмотрим данное в первой главе равенство
(5) при s=1, получим 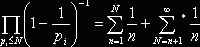 , отсюда
, отсюда 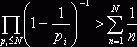 и ввиду расходимости
гармонического ряда, имеем при
и ввиду расходимости
гармонического ряда, имеем при ![]()
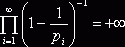 (1). Если бы количество простых чисел было конечным, то и это
произведение имело конечное значение. Однако, полученный результат
свидетельствует об обратном. Доказательство завершено.
(1). Если бы количество простых чисел было конечным, то и это
произведение имело конечное значение. Однако, полученный результат
свидетельствует об обратном. Доказательство завершено.
Теперь перепишем (1) в виде 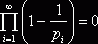 . Опираясь на теорему о сходимости бесконечного произведения, из расходимости предыдущего делаем вывод, что ряд
. Опираясь на теорему о сходимости бесконечного произведения, из расходимости предыдущего делаем вывод, что ряд ![]() расходится. Это
предложение даёт некоторую характеристику роста простых чисел. Подчеркнём, что
оно гораздо сильнее утверждения о расходимости гармонического ряда, так как
здесь речь идёт лишь о части его членов, тем более что в натуральном ряде
имеются сколь угодно длинные промежутки без простых чисел, например:
расходится. Это
предложение даёт некоторую характеристику роста простых чисел. Подчеркнём, что
оно гораздо сильнее утверждения о расходимости гармонического ряда, так как
здесь речь идёт лишь о части его членов, тем более что в натуральном ряде
имеются сколь угодно длинные промежутки без простых чисел, например: ![]() ,
, ![]() , … ,
, … , ![]() .
.
Несмотря на свою простоту приведённые выше предложения
важны в концептуальном плане, так как они начинают череду исследований всё
более и более глубоких свойств ряда простых чисел, которая продолжается по сей
день. Первоначально, основной целью изучения дзета-функции как раз и было
исследование функции ![]() , то есть количества простых чисел не превосходящих x. В качестве примера формулы, связывающей
, то есть количества простых чисел не превосходящих x. В качестве примера формулы, связывающей ![]() и
и ![]() , мы сейчас получим равенство
, мы сейчас получим равенство
![]() (2).
(2).
Сначала воспользуемся разложением дзета-функции в
произведение: 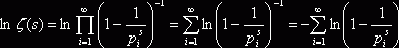 . Из логарифмического ряда
. Из логарифмического ряда ![]() , учитывая, что
, учитывая, что 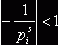 , приходим к ряду
, приходим к ряду 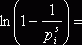
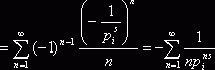 . Значит,
. Значит, ![]() .
.
Теперь вычислим интеграл в правой части (2). Так как при ![]()
![]() , то
, то 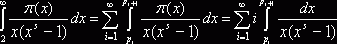 . Во внутреннем интеграле положим
. Во внутреннем интеграле положим ![]() , тогда
, тогда ![]() и
и 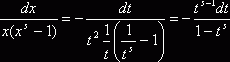 , отсюда
, отсюда 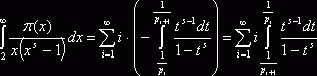 .В промежутке интегрирования
.В промежутке интегрирования ![]() , поэтому верно разложение
, поэтому верно разложение ![]() и
и ![]()
![]() . Получаем
. Получаем 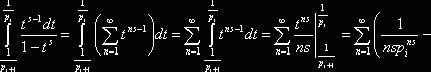
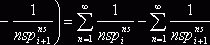 . Теперь
. Теперь 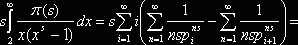
![]()
![]() . Если сравнить полученное значение интеграла с рядом для
. Если сравнить полученное значение интеграла с рядом для ![]() , то увидим, что они тождественны и равенство (2) доказано.
, то увидим, что они тождественны и равенство (2) доказано.
Используем формулу (2) для доказательства одной очень
серьёзной и важной теоремы, а именно получим асимптотический закон
распределения простых чисел, то есть покажем, что ![]() .
.
В качестве исторической справки отмечу, что великий немецкий математик Карл Фридрих Гаусс эмпирически установил эту закономерность ещё в пятнадцатилетнем возрасте, когда ему подарили сборник математических таблиц, содержащий таблицу простых чисел и таблицу натуральных логарифмов.
Для доказательства возьмём формулу (2) и попытаемся
разрешить это уравнение относительно ![]() , то есть обратить интеграл. Сделаем это с помощью формулы
обращения Меллина следующим образом. Пусть
, то есть обратить интеграл. Сделаем это с помощью формулы
обращения Меллина следующим образом. Пусть ![]()
![]() . Тогда
. Тогда
![]() (3). Этот интеграл имеет нужную форму, а
(3). Этот интеграл имеет нужную форму, а ![]() не повлияет на
асимптотику
не повлияет на
асимптотику ![]() . Действительно, так как
. Действительно, так как ![]() , интеграл для
, интеграл для ![]() сходится равномерно в
полуплоскости
сходится равномерно в
полуплоскости ![]() , что легко обнаруживается сравнением с интегралом
, что легко обнаруживается сравнением с интегралом 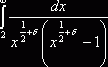 . Следовательно,
. Следовательно, ![]() регулярна и ограничена
в полуплоскости
регулярна и ограничена
в полуплоскости ![]() . То же самое справедливо и относительно
. То же самое справедливо и относительно ![]() , так как
, так как ![]()
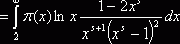 .
.
Мы могли бы уже применить формулу Меллина, но тогда было бы
весьма затруднительно выполнить интегрирование. Поэтому прежде преобразуем
равенство (3) следующим образом. Дифференцируя по s, получаем ![]() . Обозначим левую часть через
. Обозначим левую часть через ![]() и положим
и положим 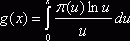 ,
, 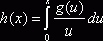 , (
, (![]() ,
, ![]() и
и ![]() полагаем равными нулю
при
полагаем равными нулю
при ![]() ). Тогда, интегрируя по частям, находим
). Тогда, интегрируя по частям, находим 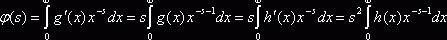 при
при ![]() , или
, или 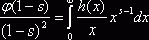 .
.
Рекомендуем скачать другие рефераты по теме: bestreferat ru, реферат современная россия.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата
 Главная
Главная