
Дзета-функция Римана
| Категория реферата: Рефераты по математике
| Теги реферата: bestreferat, сочинения по русскому языку
| Добавил(а) на сайт: Петронилла.
Предыдущая страница реферата | 1 2 3 4 5
Но ![]() непрерывна и имеет
ограниченную вариацию на любом конечном интервале, а так как
непрерывна и имеет
ограниченную вариацию на любом конечном интервале, а так как ![]() , то
, то ![]() (
(![]() ) и
) и ![]() (
(![]() ). Следовательно,
). Следовательно, ![]() абсолютно интегрируема
на
абсолютно интегрируема
на ![]() при
при ![]() . Поэтому
. Поэтому 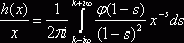 при
при ![]() , или
, или 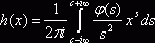 при
при ![]() . Интеграл в правой части абсолютно сходится, так как
. Интеграл в правой части абсолютно сходится, так как ![]() ограниченна при
ограниченна при ![]() , вне некоторой окрестности точки
, вне некоторой окрестности точки ![]() . В окрестности
. В окрестности ![]()
![]() и можно положить
и можно положить ![]() , где
, где ![]() ограниченна при
ограниченна при ![]() ,
, ![]() и имеет
логарифмический порядок при
и имеет
логарифмический порядок при ![]() . Далее,
. Далее, 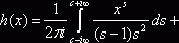
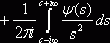 . Первый член равен сумме вычетов в особых точках, расположенных
слева от прямой
. Первый член равен сумме вычетов в особых точках, расположенных
слева от прямой ![]() , то есть
, то есть ![]() . Во втором члене можно положить
. Во втором члене можно положить ![]() , так как
, так как ![]() имеет при
имеет при ![]() лишь логарифмическую
особенность. Следовательно,
лишь логарифмическую
особенность. Следовательно, ![]() . Последний интеграл стремится к нулю при
. Последний интеграл стремится к нулю при ![]() . Значит,
. Значит,
![]() (4).
(4).
Чтобы перейти обратно к ![]() , используем следующую лемму.
, используем следующую лемму.
Пусть ![]() положительна и не
убывает и пусть при
положительна и не
убывает и пусть при ![]()
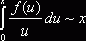 . Тогда
. Тогда ![]() .
.
Действительно, если ![]() - данное положительное
число, то
- данное положительное
число, то ![]()
![]() (
(![]() ). Отсюда получаем для любого
). Отсюда получаем для любого ![]()
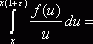
![]() . Но так как
. Но так как ![]() не убывает, то
не убывает, то 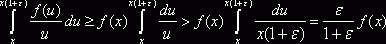 . Следовательно,
. Следовательно, ![]() . Полагая, например,
. Полагая, например, ![]() , получаем
, получаем ![]() .
.
Аналогично, рассматривая 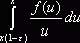 , получаем
, получаем ![]() , значит
, значит ![]() , что и требовалось доказать.
, что и требовалось доказать.
Применяя лемму, из (4) имеем, что ![]() ,
, ![]() , поэтому
, поэтому ![]() и теорема доказана.
и теорема доказана.
Для ознакомления с более глубокими результатами теории дзета-функции Римана могу отослать заинтересованного читателя к прилагаемому списку использованной литературы.
Список литературы
Титчмарш Е.К. Теория дзета-функции Римана. Череповец, 2000 г.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том II. М.,1970 г.
Привалов И.И. Введение в теорию функций комплексного переменного. М.,1999 г.
Айерленд К., Роузен М. Классическое введение в современную теорию чисел. М.,1987 г.
Шафаревич З.А. Теория чисел. М.,1986г.
Скачали данный реферат: Виленин, Ugolev, Kamenskih, Chichikov, Филофей, Фирс.
Последние просмотренные рефераты на тему: семья реферат, мировая торговля, курсовая работа по праву, реферат знания.
Категории:
Предыдущая страница реферата | 1 2 3 4 5
 Главная
Главная