Предыдущая страница реферата | 1  2  3  4  5  6  7

Эти уравнения (*) легче всего запомнить при помощи следующего правила: для того, чтобы найти точки, которые могут быть точками условного экстремума функции

Z= f(x, y) при уравнении связи j (x, y) = 0, нужно образовать вспомогательную функцию

Ф(х,у)=f(x,y)+l j (x,y)

Где l -некоторая постоянная, и составить уравнения для отыскания точек экстремума этой функции.

Указаная система уравнений доставляет, как правило, только необходимые условия, т.е. не всякая пара значений х и у, удовлетворяющая этой системе, обязательно является точкой условного экстремума. Достаточные условия для точек условного экстремума я приводить не стану; очень часто конкретное содержание задачи само подсказывает, чем является найденная точка. Описанный прием решения задач на условный экстремум называется методом множителей Лагранжа.

Метод множителей Лагранжа имеет наглядный геометрический смысл, который я сейчас поясню.

Предположим, что на рис 4. Изображены линии уровня функции Z= f(x, y) и линия L, на которой отыскиваются точки условного экстремума.

 

Если в точке Q линия L пересекает линию уровня, то эта точка не может быть точкой условного экстремума т.к. по одну сторону от линии уровня функция Z= f(x, y) принимает большие значения, а по другую - меньшие. Если же в точке P линия L не пересекает соответствующую линию уровня и, значит, в некоторой окрестности этой точки лежит по одну сторону от линии уровня, то точка P будет как раз являться точкой

условного экстремума. В такой точке линия L и линия уровня Z= f(x, y) =С касаются друг друга (предполагается, что линии гладкие). И угловые коэффициенты касательных к ним должны быть равны. Из уравнения связи j (x, y) = 0 имеем

y`=-j `x/j `y, а из уравнения линии уровня y`=-fx`/fy`. Приравнивая производные и произведя простейшее преобразование мы получим уравнение

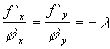Приведенное рассуждение теряет силу, если линия уровня такова, что во всех ее точках fx`=0, fy`=0. Можно рассмотреть, например, функцию z = 4-x2 и линию уровня x=0, соответствующую значению z = 4.

Можно искать условный экстремум функции f(x,y,z) при двух уравнениях связи: j 1(x, y, z) = 0 и j 2(x, y, z) = 0

Эти уравнения определяют линию в пространстве. Таким образом задача сводится к отысканию такой точки линии, в которой функция принимает экстремальное значение, причем сравниваются значения функции только в точках рассматриваемой линии.

Метод множителей Лагранжа в этом случае принимается следующим образом: строим вспомогательную функцию

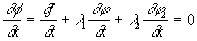
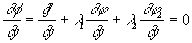Ф(x, y, z) = f(x, y, z)+l 1j 1(x, y, z) +l 2j 2(x, y, z), где l 1 и l 2- новые дополнительные неизвестные, и состовляем систему уравнений для отыскания экстремумов этой функции.

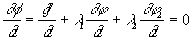Добавляя сюда два уравнения связи получаем систему уравнений с пятью неизвестными x, y, z, l 1, l 2. Искомыми точками условного экстремума могут быть только те, координаты х, у, z которых являются решением этой системы.

Список использованной литературы:

А.Ф. Бермант, И.Г. Абрамович. Краткий курс математического анализа.

Шипачев Учебник высшей математики

 

 

 

Скачали данный реферат: Filofeja, Балдин, Hramov, Фисенко, Zoja, Materov.
Последние просмотренные рефераты на тему: курсовые работы, оружие реферат, тесты для девочек, реферат по биологии.





Предыдущая страница реферата | 1  2  3  4  5  6  7