Claw.ru | Рефераты по математике | Группы преобразований Группы преобразований | Категория реферата: Рефераты по математике | Теги реферата: конспект урока культура, игра реферат | Добавил(а) на сайт: Левкович. Предыдущая страница реферата | 1  2  3 | Следующая страница реферата 1	I = (1)	Тождест-венный оператор	s = (-1)	Отраже-ние
2	=	Поворот на угол j	=	Отраже-ние
3	=	Поворот на угол j вокруг OZ	=	Зеркаль-ный пово-рот

Замечание 1.

Учитывая связь между перемещением f и оператором f*, можно утверждать, что в подходящей декартовой системе координат имеет место формула:

R = АR + v , где А - одна из матриц из таблицы, а v - некоторый вектор. Следовательно, всякое перемещение f имеет обратное , которое задается формулой R = (R - v ) = R - v. Поскольку матрица - ортогональна, обратное отображение также является перемещением. Отметим еще, что для всякой ортогональной матрицы P и любого вектора w преобразование R = PR + w является перемещением.

Замечание 2.

Имеется существенное различие между математическим понятием перемещения и физическим понятием движения. Во втором случае имеется в виду непрерывное во времени изменение положения точки, в то время как в первом фиксируются только ее начальное и конечное положения.

Перемещения с det(A) = 1 можно представлять себе и как движения, в то время как при det(A)= -1 такое представление невозможно, если оставаться в пределах исходного пространства X.

3. Классификация перемещений.

Напомним, что нам уже известны некоторые перемещения. Перемещениями прямой являются тождественное преобразование I, перенос на вектор v и отражение относительно точки О .

Для случая плоскости перемещениями будут уже упомянутые I и , а также поворот вокруг точки О на угол j и отражение относительно прямой l . Определим дополнительно скользящее отражение как комбинацию отражения относительно прямой l с переносом на вектор v½ ½ l .

Наконец, для пространства мы имеем перемещения I и , а, кроме того поворот вокруг оси, заданной точкой О и единичным направляющим вектором w на угол j и отражение относительно плоскости p . Определим дополнительно зеркальный поворот как комбинацию отражения относительно плоскости, заданной точкой О и вектором нормали n с поворотоми скользящее отражение - композицию отражения . относительно плоскости p и переноса на вектор v½ ½ p . Наконец, определим винтовое перемещение как комбинацию поворота и параллельного переноса на вектор hw .

Отметим, что некоторые из указанных выше перемещений являются частными случаями других. Например, тождественное перемещение можно рассматривать как перенос на нулевой вектор (или как поворот на нулевой угол), отражение является частным случаем скользящего отражения при v = 0 и т. д.

Теорема 3 .

Каждое перемещение f в 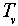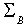(n = 1, 2, 3 ) суть одно из следующих :

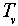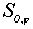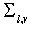n = 1 , n = 2 , , n = 3 , , .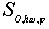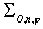

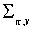Доказательство.

Как уже отмечалось, можно выбрать такой ортонормированный базис, что перемещение f имеет вид R = АR + v , где v - некоторый вектор. Если изменить начало координат : R = r + u , R = r + u , получаем: r = Ar + v , где v = Au -u +v = (A - E)u + v .Мы видим, что если число 1 не является собственным значением матрицы А (или, если угодно, оператора f*) , то можно выбрать u так, что в новой системе координат v = 0 . (Поскольку матрица A - E невырождена). Тем самым утверждение теоремы доказано при n=1 и при n=2 в случае det(A) = 1 (так как собственные значения суть exp(ij )¹ 1 при j ¹ 2 p n ).

В случае матрицы можно добиться, чтобы v = , что приводит к скользящему отражению . Для матрицы при j ¹ 2 p n получаем v = , и мы приходим к винтовому перемещению . (При j =2 p n мы приходим к переносу). Наконец, для при j ¹ 2 p n можно считать v = 0 , что приводит к зеркальному повороту , а при j =2 p n - v = и получается скользящее отражение .

Замечание. ( о параметрах перемещений)

Параметр для поворота плоскости будем считать изменяющимся mod 2 p т. е. = . Такое же соглашение будем использовать и для винтового перемещения при h > 0. Если же h = 0 , и речь идет о повороте в пространстве, надо учитывать, что = . В частности, = (отражение относительно прямой параллельной v и проходящей через О). Аналогично, = . Если при этом j = p это преобразование не зависит от вектора n и является отражением относительно точки О.

4* Композиции 1.

Теорема 4

Рекомендуем скачать другие рефераты по теме: титульный лист реферата, диплом.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата