Группы преобразований

| Категория реферата: Рефераты по математике
| Теги реферата: конспект урока культура, игра реферат
| Добавил(а) на сайт: Левкович.

Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f· g)* = f*g*(Символом · обозначена композиция перемещений).

Доказательство.

Используем координатную форму записи: f( R) = AR + v, g( R) = BR + w. Тогда: (f· g)( R) = f( (g( R)) = f( BR + w) = A( BR +w) +v = ( AB)R + ( Aw + v). Следовательно, (f· g)* = AB = f*g*.

Следствие.

Композиция двух перемещений с определителями одного знака имеет определитель (+1); если знаки определителей противоположны, композиция имеет определитель (-1).

Вычисление композиции перемещений пространства 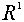не вызывает затруднений. Отметим только, что 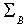· 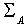= 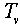,где v =2AB.

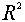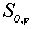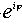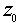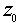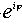
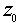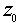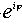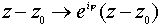Для случая пространства удобно использовать комплексные числа. Отождествляя их с точками плоскости, получаем удобный способ записи перемещений. Например, поворот можно записать в виде: z ® z + c. Точка О является неподвижной и соответствующее комплексное число находится из уравнения = + с, откуда = с/(1-). Таким образом, Отметим, что 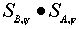= 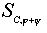при j + y ¹ 0 (mod 2 p ) . В то же время при j + y = 0 указанная композиция будет переносом на вектор AD, где D = .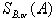

Преобразование z® 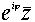+c является скользящим отражением относительно прямой Im(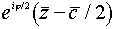= 0 на вектор 0,5 (с + 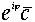). Если прямая l проходит через точку 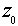и ее направляющий вектор (рассматриваемый как комплексное число) имеет аргумент 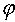, то перемещение 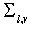можно записать в виде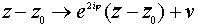

Композиция двух скользящих отражений относительно пересекающихся прямых будет поворотом. В то же время, если прямые параллельны, композиция - перенос.