Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поскольку

, то выражение 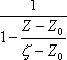 можно представить как сумму бесконечно убывающей геометрической прогрессии со знаменателем , т.е. :

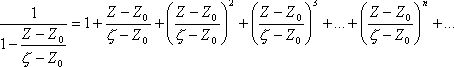
                     (12)

Представим равномерно сходящимся рядом в круге радиуса r, умножая (12) на 1/(2pi) и интегрируя по L при фиксированном  Z, получим : слева интеграл (13) который равен f (Z), а справа будет сумма интегралов :

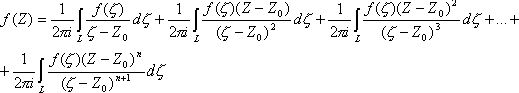
Обозначая , получим :             (14)

Это разложение функции f (Z) в круге R в ряд Тейлора. Сравнивая (14) с рядом (2) находим, что                                                                                  (15)

ТЕОРЕМА 2.

Если однозначная функция f(Z) аналитична вне круга с радиусом r с центром в точке Z0 для всех Z выполняется неравенство r < |Z-Z0 |, то она представляется рядом :

                                                                        (16)

где  h - ориентированная против часовой стрелки окружность радиуса r (сколь угодно большое число). Если обозначить   (17) , получим :

                                                (18)

ТЕОРЕМА 3.

Если однозначная функция f(Z) аналитическая в кольце Z< |Z-Z0 |<R, где  0£ Z<R<¥ , то она раскладывается в сходящийся степенной ряд :

                                  (19)

f1 и  f2 можно представить в виде двух рядов :

                              (20)

                           (21)

Ряд (19) – ряд Лорана, при этом ряд (20) сходится в круге радиуса R, ряд (21) сходится вне круга радиуса R функции f2(Z). Общая область сходимости ряда – кольцо между   r и R.

f1(Z) – правильная часть.

f2(Z) – главная часть ряда Лорана.

Ряд Тейлора – частный случай ряда Лорана при отсутствии главной его части.

Классификация изолированных особых точек. Вычеты.

Определение 1. Особой точкой функции f(Z) определенной в области (замкнутой) G, ограниченной Жордановой кривой, называется точка   Z=Z0 Î G в которой аналитичность функции  f1(Z) нарушается. Рабочая точка Z=Z0 функции f(Z), ограниченной в круге |Z-Z0|<R называется изолированной, если функция  f(Z) в каждой точке этого круга аналитична, кроме самой точки Z=Z0. В зависимости от поведения функции f(Z) в окрестности изолированных особых точек последние классифицируются на :

Рекомендуем скачать другие рефераты по теме: конспект урока 7 класс, реферат религия.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата