Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата



Далее дается само определение функции, вводятся термины аргумент и значение функции.

“В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называют функциональной зависимостью или функцией.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией от этого аргумента. Так, площадь квадрата является функцией от длины его стороны; путь, пройденный автомобилем с постоянной скоростью, является функцией от времени движения. Значения зависимой переменной называют значениями функции.

Все значения которые принимает независимая переменная, образуют область определения функции.”

Так на практике реализуется индуктивный подход к изучению функций в школе. Альтернативой ему служит дедуктивный подход, который, хотя и применяется реже, имеет целый ряд положительных аспектов, которые и стали причиной его применения в школе. Для этого подхода характерно первоначальное, полное и сжатое изложение учебного материала, пусть даже малопонятного при первом прочтении, и дальнейшая углубленная проработка всех примеров, терминов и определений. Такой подход к изучению функций и не только их позволяет учащимся самостоятельно попытаться проследить логические связи в излагаемом материале, резко увеличивает интенсивность мыслительной деятельности, способствует более активному и глубокому запоминанию. Вот как выглядит изложение той же темы “Понятие функции” в соответствии с дедуктивным подходом:

1. Зависимости одной переменной от другой называют функциональными зависимостями.

2. Зависимость переменной у от переменной х называют функцией, если каждому значению х соответствует единственное значение у. При этом используют запись у = f (х).

3. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Говорят, что у является функцией от х.

4. Значение у, соответствующее заданному значению х, называют значением функции.

5. Все значения, которые принимает независимая переменная, образуют область определения функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.

6. Для функции f приняты обозначения: D ( f ) -область определения функции, E ( f ) - множество значений функции, f (х0) - значение функции в точке х0.

7. Если D ( f ) Ì R и E ( f ) Ì R, то функцию называют числовой.

8. Элементы множества D ( f ) также называют значениями аргумента, а соответствующие им элементы E ( f ) - значениями функции.

9. Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

10. Графиком функции называют множество всех точек, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.

Затем, на следующих уроках, происходит детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры - идет усвоение нового материала.

Методика изучения прямой и обратной пропорциональной зависимости

Введение понятий прямой и обратной пропорциональной зависимости является важным шагом на пути к введению понятия функциональной зависимости и в дальнейшем к изучению линейной и обратной функций. Используя на практике индуктивный подход и знания о пропорции, полученные учениками, преподаватель на нескольких примерах может подвести учеников к пониманию понятий прямой и обратной пропорциональной зависимости.

Например:

«Члены пропорции обладают свойством, которое называют основным свойством пропорции. Во всякой пропорции произведение крайних членов равно произведению средних членов, то есть если a/b=c/d , то a · d = b · c . Это свойство применяется при нахождении неизвестного члена пропорции.

Пусть a/x = c/d , то x = a · d/c .

Посмотрите, как можно использовать знания математики в русском языке!

Именительный падеж - кто? что?

Родительный падеж - кого? чего?

Дательный падеж - кому? X ?

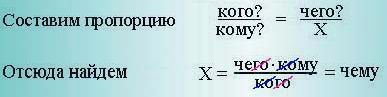
Рекомендуем скачать другие рефераты по теме: реферат деловой, шпаргалки по экономике.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата