
Конспекты лекций по математической логике
| Категория реферата: Рефераты по математике
| Теги реферата: реферат статус, изложение по русскому языку 6
| Добавил(а) на сайт: Анохин.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата
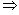 это элементарно
это элементарно 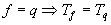
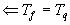 возьмем набор
возьмем набор 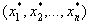
а) 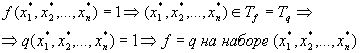
б) 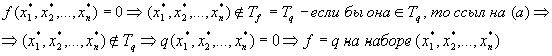
Доказательство: 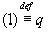 , будем доказывать, что
, будем доказывать, что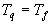 .
.
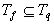 . Возьмем
. Возьмем 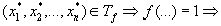 он попадает в число суммируемых наборов и по нему будет проводиться сумирование.
он попадает в число суммируемых наборов и по нему будет проводиться сумирование.
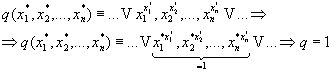
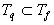 . Возьмем другой набор из
. Возьмем другой набор из 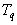
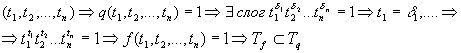
Следовательно 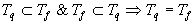
2.2.3 Некоторые другие виды ДНФ.
Опр: 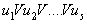 - называется минимальной ДНФ, если она имеет
- называется минимальной ДНФ, если она имеет 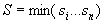 - наименьшую возможную длину из всех ДНФ данной функции.
- наименьшую возможную длину из всех ДНФ данной функции.
Опр: 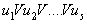 - называется тупиковой ДНФ, если из неё нельзя выбросить ни одного слагаемого с сохранением булевой функции.
- называется тупиковой ДНФ, если из неё нельзя выбросить ни одного слагаемого с сохранением булевой функции.
(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не верно.)
Опр: К-мерной гранью называется такое подмножество 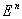 , которая является носителем некоторой элементарной конъюнкции длины: n-k.
, которая является носителем некоторой элементарной конъюнкции длины: n-k.
Опр: Предположим дана функция 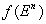 и есть
и есть 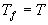 . Грань называется отмеченной, если она целиком содержится в носителе Т.
. Грань называется отмеченной, если она целиком содержится в носителе Т.
Опр: Максимальная грань – это такая грань, которая не содержится ни в какой грани более высокой размерности.
Предложение: Любую отмеченную грань можно вложить в максимальную грань.
Предложение: 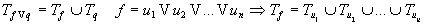
(Носитель любой функции можно разложить в объединение нескольких граней разной размерностей)
Предложение: Носитель любой функции разлагается в объединение всех своих максимальных граней. 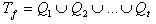
Опр: Элементарная конъюнкция называется минимальной, если её носитель является максимальной гранью. Следовательно всякая булева функция разлагается в дизъюнкцию всех своих элементарных конъюнкций.
Опр: Сокращенная ДНФ – разложение данной булевой функции в соответствующие ДНФ, которые соответствуют объединению её максимальных граней.
Теор: Минимальная ДНФ может быть получена из сокращенной отбрасыванием некоторого количества слагаемых, возможно пустого.
3 Логические Исчисления. 3.1 Исчисления высказывания (ИВ).3.1.1 Определения.
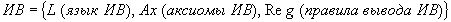
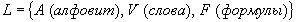
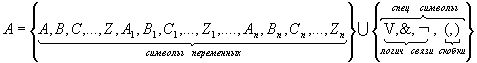
Опр: V – словом в алфавите А, называется любая конечная упорядоченная последовательность его букв.
Рекомендуем скачать другие рефераты по теме: изложение 3, пушкин реферат.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата
 Главная
Главная