для
l = 0,1,2,... - назовем нормированным следом u(x,y) в точке (x0,0) аналогично
его определению в [4].
Ортонормированному
базису {ek,fk} сопоставим бесконечную матрицу 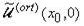 , столбцы
которой являются нормированными следами в (x0,0) функций ek и fk. Матрица
, столбцы
которой являются нормированными следами в (x0,0) функций ek и fk. Матрица 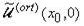 - это
нормированная фундаментальная матрица следов (ФМС) в точке (x0,0). Из [4]
известно, что
- это
нормированная фундаментальная матрица следов (ФМС) в точке (x0,0). Из [4]
известно, что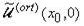 разложима в
произведение трех сомножителей, первый из которых Q = (qij) частично
изометричен в l2, второй - диагонален с положительной возрастающей
последовательностью диагональных элементов {j}, а третий -
изометричен в l2, т.е.
разложима в
произведение трех сомножителей, первый из которых Q = (qij) частично
изометричен в l2, второй - диагонален с положительной возрастающей
последовательностью диагональных элементов {j}, а третий -
изометричен в l2, т.е.
Учитывая
параметры этого разложения и формулы нахождения коэффициентов ряда [4, §5, теорема 1] и используя свойства скалярного произведения, канонический в точке
(x0,0) базис 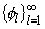 удобно
записать в виде ряда по функциям ek и fk. Тогда при всех натуральных l имеют
место равенства:
удобно
записать в виде ряда по функциям ek и fk. Тогда при всех натуральных l имеют
место равенства:
|
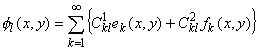
|
(3.2)
|
|
где 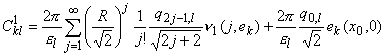 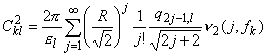
|
(3.3)
|
Дифференцирование
ek и fk сводится к дифференцированию uk и vk.
4. Приближенное интегрирование гармонических
функций
В
этом параграфе построим формулы интегрирования произвольной функции из W(S)
и базисной последовательности полиномов.
Теорема
4.1. Существует единственная последовательность 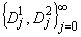 такая, что для
любой функции u из W(S) и точки (x0,0) луночки S скалярное произведение
такая, что для
любой функции u из W(S) и точки (x0,0) луночки S скалярное произведение
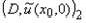 конечно и при
этом
конечно и при
этом
|
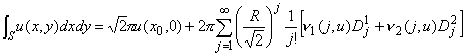
|
(4.1)
|
Последовательность
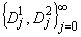 вычисляется по
формулам:
вычисляется по
формулам:
|
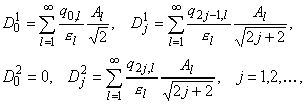
|
(4.2)
|
где
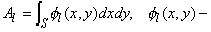 базис в W(S).
базис в W(S).
Это
утверждение легко доказать, если разбить функцию u(x,y) на две части - четную и
нечетную по y и разложить каждую в ряд по каноническому базису W(S).
Далее, учитывая определение (3.1) координат вектор-столбца 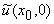 , производя
необходимые преобразования с суммами и учитывая (3.2)-(3.3), получим формулы
(4.1).
, производя
необходимые преобразования с суммами и учитывая (3.2)-(3.3), получим формулы
(4.1).
В
формулировке теоремы 4.1 мы вывели представления для коэффициентов D1j и D2j, которые используют интегралы по луночке S. Численное вычисление множителя Al
сводится к результатам следующего утверждения. Но сначала условимся об
обозначениях.
Теорема
4.2. Интеграл от полинома uk+1, взятый по луночке S = S(1,2-1), совпадает с приращением функции Qk() на отрезке [1,2], а от полинома vk+1, взятый по той же луночке, равен нулю.
Здесь
отметим, что приведенное в §4 приложение системы полиномов является не
единственным. Например, ее можно применять в задачах, использующих
альтернирующий метод Шварца. Также с их помощью можно находить решения в
составных областях на плоскости.
Список литературы
Рекомендуем скачать другие рефераты по теме: диплом, вулканы доклад.
Предыдущая страница реферата |
1
2
3
4 |
Следующая страница реферата

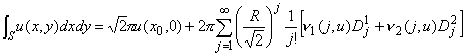
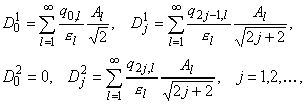
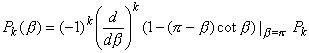
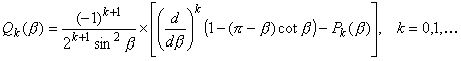
 Главная
Главная