Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

(27)

и линейное приближение эффекта Доплера

, ( 28)

то получится взаимосвязь звёздной величины m с красным смещением z и постоянной Хаббла H

. (29)

Поскольку измерения производятся, как правило, для каких-то одинаковых объектов (определённых типов галактик, звёздных скоплений, ярчайших звёзд), то для каждого из них сумма также будет являться постоянной величиной. И действительно, результаты измерений красных смещений спектров излучения галактик в своей наиболее достоверной части дают следующую формулу

, (30)

где скорость света берётся в км/с.

После выведения из-под знака логарифма скорости света данное выражение принимает вид

. (31)

Таким образом, можно считать, что мы имеем теоретически выведенное выражение (25) и найденное из наблюдений его линейное приближение (31).

Действительно, разложение в ряды входящих в (25) компонентов и ограничение длины рядов только линейными членами, показывает, что (31) действительно является линейным приближением для (25).

Правые части обеих вышеуказанных зависимостей приведены к одинаковому виду, при котором каждая из них состоит из суммы функции от z и некоторой константы. Поэтому естественно считать, что данные константы равны друг другу, т. е. что A=21,68, как это следует из наблюдений.

Тогда с учётом нового закона распространения света и проведенных рассуждений зависимость “видимая звездная величина m — красное смещение z спектров излучения галактик” (диаграмма Хаббла) приобретает вид:

. (32)

Интересно проследить поведение зависимости (32) при различных значениях z. Так, в диапазоне наблюдаемых значений z данная зависимость практически линейна (рис. 3а), что полностью согласуется с результатами внегалактических наблюдений.

Для больших значений функция (32) носит явно нелинейный характер (рис. 3б). Нелинейности начинают проявляться при или . Поэтому естественно, что наиболее удалённые наблюдаемые объекты Вселенной должны перестать удовлетворять соотношению (30) и следующему из него выражению (31).

Следует также отметить, что в работe [3] приведены результаты исследований спектров излучения квазаров, в которых выявлено циклическое изменение спектральной плотности, пропорциональное аргументу ln(1+ z). Такое распределение коррелирует с распределением галактик, образующих во Вселенной однородные тонкостенные скопления в виде сот или пены.

С учётом формулы (24) циклическое изменение спектральной плотности излучения квазаров преобразуется в циклическую зависимость распределения квазаров по расстояниям, указывающую на однородность Вселенной не только в пространстве, но и во времени, т. е. на её стационарность за последние минимум 30 млрд. лет (столько времени до нас шли электромагнитные волны от самых далёких квазаров).

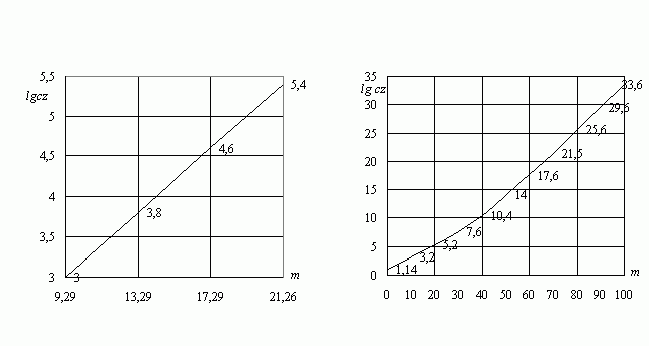
Рис. 3. Диаграмма Хаббла для различных диапазонов красных смещений

Заключение

Таким образом, на основании приведенного анализа видно, что микроволновое фоновое излучение космоса действительно не является убедительным доказательством существования Большого Взрыва Вселенной, так как оно может быть всего лишь равновесным излучением всех звёзд стационарной Вселенной при наличии диссипации энергии электромагнитных волн в соответствии с формулой (1). Окончательный же ответ о природе микроволнового фона космоса может быть получен только после постановке лабораторного эксперимента по проверке самой этой формулы. Схема такой установки автором уже предложена [1]. Остаётся найти партнёров и финансирование.

Список литературы

Жук Н. А. Космологические решения уравнений Эйнштейна. — Авторское свидетельство № 1718 с приоритетом от 28.01.99 (Украина).

Жук Н. А. Космология. — Харьков: ООО “Модель Вселенной”, 2000, 464 с.

Karlsson K. G. Possible discretization of quasar redshifts. // Astron. and Astrophys., 1971, v. 13, p. 333-335.

Рекомендуем скачать другие рефераты по теме: скачать реферат человек, организм реферат.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата