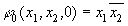
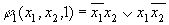
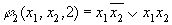
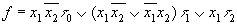
Временные булевы функции применяются для описания работы схем с памятью.
Определение: Производной первого порядка от булевой функции 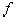 по переменной
по переменной 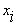 называется выражение:
называется выражение: 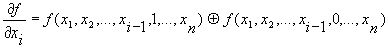
Где первая 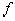 - единичная остаточная функция, а вторая- нулевая остаточная функция.
- единичная остаточная функция, а вторая- нулевая остаточная функция.
Пример:
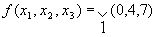 после минимизации получим:
после минимизации получим:
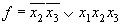
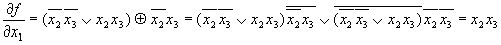
производная первого порядка по 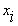 переменной определяет условие, при котором эта функция изменяет свое значение при перемене значения
переменной определяет условие, при котором эта функция изменяет свое значение при перемене значения 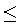 с 0 на 1.
с 0 на 1.
Для данной функции получим схему:
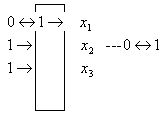
Смешанные производные k-го порядка.
Определение: смешанной производной k-го порядка называется выражение вида:
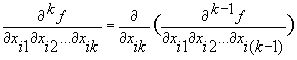
При этом порядок фиксированной переменной не имеет значения. Производная k-го порядка 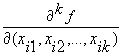 определяет условия, при которых эта функция изменяет свое значение при одновременном изменении значений
определяет условия, при которых эта функция изменяет свое значение при одновременном изменении значений 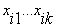 .
.
Согласно Бохману, производная k-го порядка вычисляется по формуле:
Рекомендуем скачать другие рефераты по теме: культурология, конспект по окружающему миру.
Предыдущая страница реферата |
9
10
11
12
13
14
15
16
17
18
19 |
Следующая страница реферата

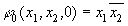
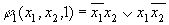
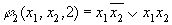
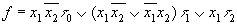
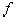 по переменной
по переменной 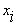 называется выражение:
называется выражение: 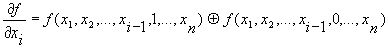
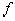 - единичная остаточная функция, а вторая- нулевая остаточная функция.
- единичная остаточная функция, а вторая- нулевая остаточная функция.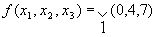 после минимизации получим:
после минимизации получим: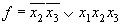
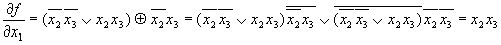
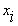 переменной определяет условие, при котором эта функция изменяет свое значение при перемене значения
переменной определяет условие, при котором эта функция изменяет свое значение при перемене значения 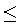 с 0 на 1.
с 0 на 1.
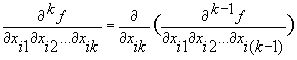
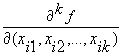 определяет условия, при которых эта функция изменяет свое значение при одновременном изменении значений
определяет условия, при которых эта функция изменяет свое значение при одновременном изменении значений 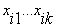 .
. Главная
Главная