Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11

6. Размер тела волны поиска (массив закрытых вершин) на заключительной итерации.

7. Число итераций.

8. Число элементов в волне на момент завершения поиска (сумма пятой и шестой характеристик).

9. Целенаправленность (число ребер в пути, деленное на восьмую характеристику, не считая начальной вершины).

10. Максимальная длина фронта волны поиска (массива открытых вершин).

Для характеристики сложности всего графа могут использоваться гистограммы указанных выше характеристик для выбранного тестового набора задач (в которые могут входить и все возможные задачи на данном графе). Численные эксперименты показали, что для алгоритмов выбора пути по априорно известному графу выполняется свойство несравнимости любых двух алгоритмов даже в пределах достаточно узкого множества возможных задач. Это означает, что если рассматриваются 2 алгоритма А и В, то существует задача, где алгоритм А эффективнее алгоритма В, и существует задача, где алгоритм В эффективнее алгоритма А.

Для исследования алгоритмов выбора пути в условиях неопределенности на террайнах могут использоваться три способа. Первый заключается в том, что на террайне выделяется конечный магистральный граф, для которого может использоваться указанный выше подход.

Второй способ заключается в построении характеристик структуры террайна.

Поскольку террайн представляет собой граф с континуумом вершин и ребер, построенных на основе отношений видимости, то на нем могут быть аналогично определены следующие две основные структурные характеристики графа: диаметр и число доминирования.

Целочисленная метрика k(x,y), задаваемая на точках носителя террайна определяется как минимальное число ребер в допустимом пути (ломаной) из x в y и наоборот. Максимум этой функции по точкам x, y и определяет диаметр террайна. Таким образом, диаметр террайна равен минимально необходимому числу сеансов измерений для передвижения между любыми двумя выбранными точками (в случае, если нет ограничений на радиус действия измерительной системы). Ниже эта характеристика будет обозначаться как γ(V).

Аналогом числа доминирования для террайна является навигационное число. Пусть А – множество точек на террайне, а V – носитель террайна. Если V(A)=V (это означает, что множество видимых из А вершин совпадает со всем террайном), то А называется навигационным множеством. Навигационное множество называется навигационным базисом, если при удалении из А любого элемента оставшееся подмножество точек уже не является навигационным.

Нетрудно видеть, что навигационное множество есть аналог доминирующего множества для конечного графа, а навигационный базис – аналог независимого доминирующего множества. Соответствующие термины для террайна подчеркивают тот факт, что ориентиры на местности должны образовывать навигационое множество для того, чтобы привязка по этим ориентирам была всюду определена.

Навигационное множество называется навигационным множеством k-го порядка, если для любой точки x |A(x)|≥k

Для стандартного террайна множество вершин Р является навигационным множеством по крайней мере четвертого порядка. Пусть nmin(V) и nmax(V) соответствуют минимальной и максимальной возможным размерностям (числу элементов) для навигационного базиса. Очевидно, что эти два числа могут быть различны (см. рис.1).

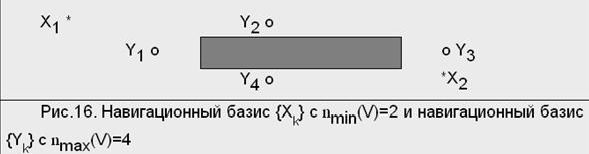
Рисунок 1

Указанные числа называются минимальным и максимальным навигационными числами террайна.

Список литературы

Райфа Г. Анализ решений. Введение в проблемы выбора в условиях неопределенности. М.: Наука, 1977.

Кирильченко А.А. Обоснование алгоритмов выбора пути в условиях неопределенности. // Препринт Ин-та прикл. матем. им. М.В. Келдыша АН СССР, 1991, N 108, 25 с.

Кирильченко А.А. Об исследовании эффективности алгоритмов выбора пути в условиях неопределенности. 2. Атлас особых ситуаций и атлас "неустойчивого доминирования" //М.:Препринт Ин-та прикл.матем. им. М.В. Келдыша РАН, 1997, N 44.-27с.

Гафт М.Г. Принятие решений при многих критериях.

Кини Р.Л., Райфа Х. Принятие решений при многих критериях.

Скачали данный реферат: Вязьмитин, Хлебников, Konrad, Magda, Bogdana, Астра.
Последние просмотренные рефераты на тему: классификация реферат, шпаргалки по русскому, экономические рефераты, изложение 3 класс.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11