
Новая модель эволюции вселенной
| Категория реферата: Рефераты по математике
| Теги реферата: конспект 2 класс, бесплатные шпаргалки по праву
| Добавил(а) на сайт: Maslov.
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата
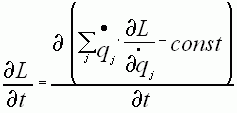 , а
производная постоянной равна нулю
, а
производная постоянной равна нулю 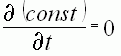
Подставляем
значения![]() в выражение
в выражение 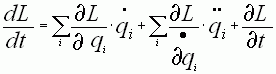 в итоге
в итоге
получаем:
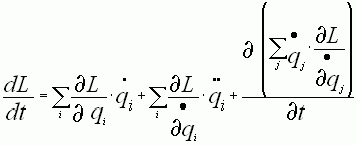 заменяя
последнее слагаемое на выражение
заменяя
последнее слагаемое на выражение 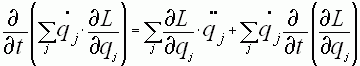 в итоге
получим следующее:
в итоге
получим следующее: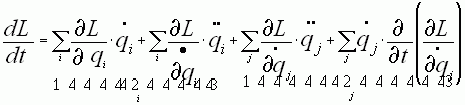 , где над
первой скобкой идёт суммирование по i, а над второй – по j.Из уравнения
движения
, где над
первой скобкой идёт суммирование по i, а над второй – по j.Из уравнения
движения 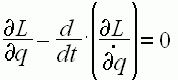 выразим
значение
выразим
значение 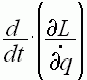 через
через ![]() Тогда общее уравнение
движения примет вид:
Тогда общее уравнение
движения примет вид: 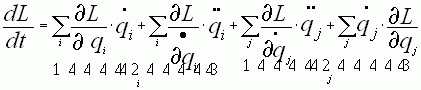 . Функция
Лагранжа и её частные производные имеют вид:
. Функция
Лагранжа и её частные производные имеют вид: 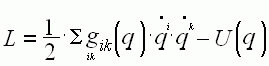 ,
, 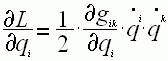 ,
, 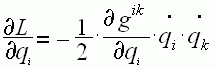 ,
, 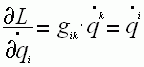
Подставляем в наше уравнение
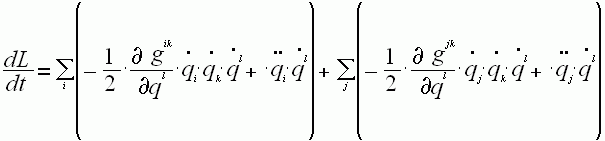
вынося
множитель ![]() из-за скобок и
для поднятия индекса умножаем всё выражение на
из-за скобок и
для поднятия индекса умножаем всё выражение на ![]() .
. ![]() ,
, 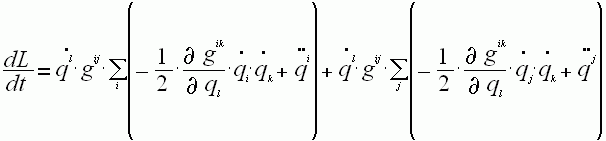 и зная условие
закона сохранения движения
и зная условие
закона сохранения движения  .
.
Тогда
разделяя первые и вторые производные и произведя замену частных производных
метрического тензора на символы Кристоффеля, (известно то, что в символах
Кристоффеля 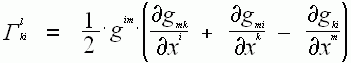 и
и ![]()
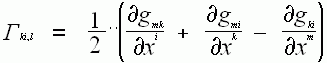 меняя местами
индексы m и i, в третьем и первом членах, в скобках, видим оба эти члена взаимно
сокращаются, так что
меняя местами
индексы m и i, в третьем и первом членах, в скобках, видим оба эти члена взаимно
сокращаются, так что 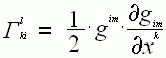 ). В нашем
случае, проделаем обратную “операцию”, заменим частные производные метрического
тензора на полновесные символы Кристоффеля.
). В нашем
случае, проделаем обратную “операцию”, заменим частные производные метрического
тензора на полновесные символы Кристоффеля.
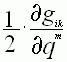 на
на ![]() , далее вынося
из под скобок вторые производные обобщённых координат
, далее вынося
из под скобок вторые производные обобщённых координат
![]() и сокращая на
и сокращая на ![]() , в итоге
получим
, в итоге
получим
![]() ,
,
где
![]() ускорение
частицы под воздействием стационарного искривления пространства-времени
(скопление Масс Вещества),
ускорение
частицы под воздействием стационарного искривления пространства-времени
(скопление Масс Вещества),
![]() дополнительное
ускорение частицы под воздействием фактора изменения энергии в этом объёме
пространства-времени.
дополнительное
ускорение частицы под воздействием фактора изменения энергии в этом объёме
пространства-времени.
![]() - связность
(символы Кристоффеля), определяющая искривленность пространства-времени под
воздействием скопления Масс Вещества.
- связность
(символы Кристоффеля), определяющая искривленность пространства-времени под
воздействием скопления Масс Вещества.
![]() - связность –
определяющая искривленность пространства-времени под воздействием фактора
изменения энергии в этом объёме пространства-времени.
- связность –
определяющая искривленность пространства-времени под воздействием фактора
изменения энергии в этом объёме пространства-времени.
# 6. Здесь приводится пример, когда рассматривается свободная частица, движущаяся в поле тяготения, в котором она (частица) получает ускорение, проекции которого на координатные оси выражаются:
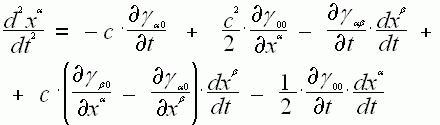
Это ускорение зависит, как мы видим, от местоположения частицы и от времени, а также от её скорости движения. Где:
![]() - ускорение
частицы (проекция ускорения на координатные оси),
- ускорение
частицы (проекция ускорения на координатные оси),
![]() - скорость
движения частицы (проекция скорости на координатные оси),
- скорость
движения частицы (проекция скорости на координатные оси), 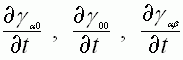 - изменение
компонент метрического тензора по времени,
- изменение
компонент метрического тензора по времени, 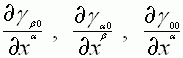 - изменение
компонент – по расстоянию.
- изменение
компонент – по расстоянию.
В
поле тяготения, которое не меняется со временем (стационарный случай), все
частные производные метрического тензора по времени равны нулю, то выражение
ускорения частицы примет вид: 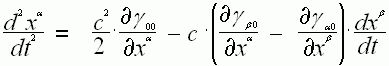
А
если ещё поле тяготения имеет центральную симметрию, то есть 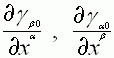 его компоненты
равны нулю, то ускорение движения частицы принимает классический вид:
его компоненты
равны нулю, то ускорение движения частицы принимает классический вид: 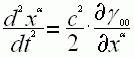 , где
, где
![]() - градиент
поля тяготения.
- градиент
поля тяготения.
# 7. Обратимся к распространению света в пустоте. Пусть
![]() - мировой
волновой вектор,
- мировой
волновой вектор, ![]() -
Хронометрическая Инварианта циклической частоты. Тогда
-
Хронометрическая Инварианта циклической частоты. Тогда ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Имеем
. Имеем
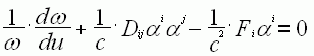 (9)
(9)
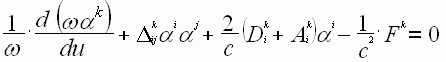 (10)
(10)
Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, реферат на тему экономика.
Категории:
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата
 Главная
Главная