Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

что  FCD=.

По теореме косинусов

FD2=FC2+СD2-2FC· СDcos  (AD–BC)2=AB2+СD2– AB· СD. (1)

Так как в трапецию ABCD можно вписать окружность, то

AD+BC=AB+CD  (AD+BC)2=(AB+СD)2. (2)

Разделив равенство (1) на равенство (2), получим

.

Разделив далее числитель и знаменатель левой дроби на произведение AD· BC, а правой части - на AB· СD, получим

.

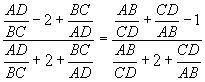Откуда, положив =t, и учитывая, что =10, имеем t=7.

В этой задаче при неудачном выборе решения оно может оказаться очень громоздким.

Весьма поучительно, на наш взгляд, решение следующей задачи.

Задача 6. В прямоугольном треугольнике АВС из вершины прямого угла С проведена биссектриса CL и медиана СМ. Найти площадь треугольника АВС, если LM=a, CM=b.

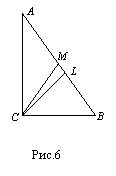Пусть АС=х и ВС=у , где х>y (рис.6), тогда х2+у2=4b2, и по свойству биссектрисы  LB=AB= и, следовательно, ML=MB–LB=b–=.

Таким образом, приходим к системе

.

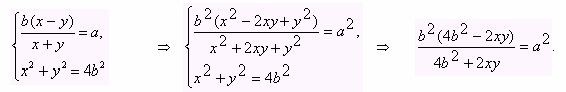Решая это уравнение относительно ху, находим S ABC= =.

Следует обратить внимание учащихся на то, что из полученной системы уравнений искать значения переменных х и · у совершенно излишне.

Задача 7. Основание равнобедренного треугольника равно 10 см, проведенная к нему высота - 12 см. Вершины треугольника служат центрами кругов, каждый из которых касается двух других внешним образом. Найти радиусы кругов, которые касаются трех указанных кругов внешним и внутренним образом.

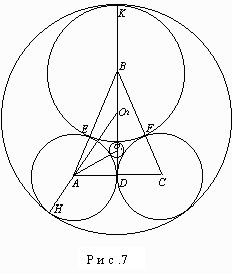Пусть e, f, d, k, h - точки касания, радиус окружности с центром в точке О1 равен r, а с центром в точке О2 - R (рис.7). Так как AD=5, АВ=13,

то BE=8, BО1=8+r, AО1=5+r, О1D=4–r.

Из прямоугольного треугольника AO1D (5+r)2=25+(4–r)2, 18r=16, r=.

ВО2=R–8, О2D=12–(R–8)=20–R, О2A=R–5,

и, следовательно, из прямоугольного треугольника АО2D имеем

(R–5)2=(20–R)2+25  R==13.

Рекомендуем скачать другие рефераты по теме: шпаргалки по математике, мировая торговля.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата